Canavan Disease: Task 10 - Normal Mode Analysis

Normal Mode Analysis is a way to predict the dynamics in a protein. Here normal mode analyses are used, since they are very memory reducing compared to typical molecular dynamics simulations.

Background

<figure id="eigen">

Eigenvalues of WEBnm@ starting with mode 7.

</figure>

There are several servers available, which can give some indication of movements and dynamics within the protein. There are three main approaches to do this:

• Molecular Dynamics (MD)
• Normal Mode Analysis (NMA)
• Elastic Network Models

The main problem using Molecular Dynamics is the CPU-Power. The calculation of dynamics in a protein depends on the timeframe (micro-, nano-, pico or even femtoseconds). The smaller the timeframe is chosen the better is the prediction in the end, but on costs of CPU Power.
A much faster approach is Normal Mode Analysis (see References). The lowest energy levels always represent the formations the protein is able to make. To calculate the modes, a Hessian Matrix is calculated within the analysis, since its eigenvectors represent the "normal modes". Those with the lowest frequencies (soft modes) are the best normal modes, since they describe the largest movements. The eigenvalues of the vectors are the squared frequencies (compare <xr id="eigen"></xr>). There are also zero-frequency modes, which represent the global movement of the protein (in WEBnm@ and NOMAD the first six). As it can be seen in the results of WEBnm@, the deformation energies, which represent the low-frequency movements are increasing with increasing mode. Taking Elastic Network Models into account, as NOMAD does, the calculation in finding the best energy level to start, is much easier. An elastic network represents a set of harmonic potentials between atoms. The CPU-Power is not affected as much as in Molecular Dynamics, the prediction on the other hand is not as distinctive as in Molecular Dynamics.

For this Task two servers WEBnm@ and NOMAD were used to calculate normal modes of aspartoacylase using the PDB-structure 2O4H. The severs provide different possibilities calculating the normal modes. <xr id="servers"></xr> gives an overview of the differences and similarities between the servers:

<figtable id="servers">

Differences and Similarities in WEBnm@ and NOMAD
Comparison	Webnm@	NOMAD
Background (see References)	WEBnm@ is using the MMTK package: MMTK calculates the low-frequence domain movements using an approximate normal mode calculation method by Hinsen et al. 200 modes are calculated for proteins with less than 1200 residues. Proteins with more than 1200 residues (N>1200) will bring N/6 modes. Only the lowest frequency modes should be taken into account. Therefore WEBnm@ presents the modes 7-12 to its users.	NOMAD makes its calculation using Elastic Network Models (or classical force fields): The Elastic Network Models (ENM) bring the advantage that a prior energy minimization to find the eigenvectors in the Hessian Matrix is not needed. The ENMs represent a set of harmonic potentials between atoms. This state represents the global minimum. Up to 160 modes are allowed to be calculated. The user has the possibility to choose how many modes.
	Calculation implies the use of the Hessian Matrix, since its eigenvectors represent the normal modes. The first 6 (zero-frequency) modes represent the global rotation and translation of the protein
Which part of the structure is taken into account for the calculation?	C-alpha atoms only
	-	2 further options: all atoms, sidechains only
Which analysis tools are available?	visualization, fluctuations, eigenvalues
	deformation energies, atomic displacements, correlation matrix	frequencies, overlap coefficients, structure minimization using GROMACS (only structures with less than 3000 atoms)
What options do I have?	choosing chain of protein, Comparative Analysis	Number of modes to calculate (first six ones are translation and rotation), distance weight (for elastic constant), ENM Cutoff (for mode calculation), Average Rmsd (in output trajectories)

Comparison of the servers WEBnm@ and NOMAD with respect to their background, calculation procedure, tools and options.

</figtable>

WEBnm@

This section shows the result of WEBnm@. The first column describes the mode. The second shows a vector-like representation on aspartoacylase. The third is the movement and at last displayed is the atomic displacement / fluctuation curve. The atomic displacement / fluctuation curve always shows which atoms do a major movement (not considered directions):

Mode 7: Deformation Energy: 1429.83 Hinge movement of two rigid protein parts, the bottom left loop region and the upper right helix/sheet region.
Mode 8: Deformation Energy: 1740.31 A small hinge movement between the bottom left loop region and the rest of the protein additionally to an inwards turning movement of the loop region.
Mode 9: Deformation Energy: 2545.68 The bottom left loop region and the upper right helix/sheet region describe a hinge movement that is orientated towards the back of the visible plane.
Mode 10: Deformation Energy: 3584.30 The motion visible for mode 10 is best described as a form of the protein tightening itself around the binding site. During that process the most flexible part seems to be the loop region in the bottom left area.
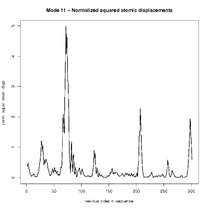
Mode 11: Deformation Energy: 4202.00 Mode 11 describes a breathing movement of the upper part of the protein. The lower left loop region is on the contrary to the other modes one of the most rigid parts of the protein.
Mode 12: Deformation Energy: 5480.10 In mode 12 a combined breathing and stretching of the whole protein is visible. The area around the binding site seems to be almost unaffected and very rigid, whereas the surface parts of the protein are more flexible.

Since aspartoacylase has a bound zinc ion, a comparison using a structure without the ligand was necessary. Therefore the ligand was deleted from the PDB-structure. To check for differences the correlation matrix (<xr id=correlation></xr>) and the normalized fluctuation of the protein (<xr id=fluctuation></xr>) were compared with the ones build for the structure without the ligand. There was no difference detectable. This may be due to the fact, that the zinc is important for the function, however not important as a stabilizing factor and the stabilization that occurs at the active site is determined mainly by secondary structure elements.

</figure>

</figure>

Correlation matrix over all modes calculated by WEBnm@ for 2O4H. The matrix displays the movement correlation between residues.

Normalized fluctuation for all modes of 2O4H. This graph summarizes which parts of the protein have a high and low movement fluctuation within the protein.

<figure id="correlation">

<figure id="fluctuation">

NOMAD

NOMAD has the possibility to choose whether the prediction should be calculated on the backbone, only on sidechains, or on all atoms. Here the calculation was done for all atoms. The result for modes 7 to 12 are shown below. The first column describes the mode, the second shows the movement and the third displays the fluctuation curve. As in WEBnm@ the atomic displacement / fluctuation curve always shows which atoms do a major movement (not considered directions). Other than in WEBnm@ here all atoms were taken into account.

Mode 7: The motion of the protein completely centers around the binding pocket. Overall it is a seesawing motion of all parts towards the centre with the most flexible part being the bottom left loop region. The secondary structure elements are the most rigid parts.
Mode 8: In mode 8 a hinge-like motion is detectable, that is centering around the active site of the protein. It looks like a clamming of the protein towards the potential substrate. The outer loopregions are the most flexible parts of the protein, whereas the secondary structure elements are the most stable.
Mode 9: Mode 9 is sort of a combination of the clamming movement of mode 8 and the seesaw movement of mode 7. Again the motion seems centered around the binding pocket of the protein.
Mode 10: Like mode 8 this mode has a hinge-like motion with the difference to mode 8 being that the imaginary plane that defines the hinge movement is orientated differently. As with the other modes the motion is centered around the binding pocket and the most flexible part is the loop region in the bottom left.
Mode 11: The motion of mode 11 is best described as if three horizontal planes exist defining the motion of the protein. The plane in the middle is moved horizontally while the other two are almost fixed in their motion. The most rigid part is centred around the binding pocket whereas the most flexible part is the loop region.
Mode 12: Mode 12 combines the clamming motion of mode 8 and 10 with a breathing of the protein. Interpreting this motion tends to give the same result as before, with motion surrounding the active site, and the loop region being the most flexible one.

Comparison

Comparing all modes calculated by both methods demonstrates that the least motion happens at the binding pocket of the protein. This is visually detectable from the Pymol representation of the modes as well as from the corresponding fluctuation curves. Especially the normalized fluctuation curve over all modes highlights this observation. Additionally it can be seen that the most flexible part of the protein is the loop region ranging approximately form residue 225 to residue 270. Although comparing the corresponding modes by Webnm@ and Nomad does not always result in the same motion, the fluctuation curves do correlate. Looking at the lower numbered modes it may be assumed that there are two domains one being the loop region. However this clear separation of movement blurs into an overall movement of the protein if looking at the higher numbered modes. Therefore it can be assumed that the protein has no separate multiple domains but is made up out of only one domain. Comparing this assumption with the annotations in Pfam and CATH the one domain theory can be validated.

References

official papers:

• WEBnm@
• NOMAD

Tasks

• Link to Task 01: Canavan Disease
• Link to Task 02: Alignments
• Link to Task 03: Sequence-based Predictions
• Link to Task 04: Structural Alignments
• Link to Task 05: Homology Modelling
• Link to Task 06: Protein Structure Prediction from Evolutionary Sequence Variation
• Link to Task 07: Researching SNPs
• Link to Task 08: Sequence-based Mutation Analysis
• Link to Task 09: Structure-based Mutation Analysis
• Link to Task 10: Normal Mode Analysis