Task 10: Molecular Dynamics Analysis
In this task we are going to analyze the results of the molecular dynamics simulations of task 8. A detailed task description can be found here. The analysis focuses on this tutorial.
Contents
Native
A BRIEF CHECK OF RESULTS
In order to verify that our simulation ran successfully we used the command line tool gmxcheck. we executed it as follows for our .xtc file:
gmxcheck -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc
How many frames are in the trajectory file and what is the time resolution?
We observed 2001 frames with a time resolution of 5ps.
How long did the simulation run in real time (hours), what was the simulation speed (ns/day) and how many years would the simulation take to reach a second?
The simulation ran 4h00:39 and had a simulation speed of 59.835 ns/day. To calculate 1 second we would need (1 / (59 * (10^(-9)))) / 365 = 46 436.0344 years
Which contribution to the potential energy accounts for most of the calculations?
- potential energy: -4.57312e+05 kJ/mol
VISUALIZATION OF RESULTS
We extracted 1000 frames from the trajectory (-dt 10), leaving out the water (selected Protein when asked for a selection). Moreover, we will remove the jumps over the boundaries and make a continuous trajectory (-pbc nojump):
trjconv -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -o protein.pdb -pbc nojump -dt 10
After that we opened the generated protein.pdb file with pymol. Here we changed the coloring to spectrum by typing the following to the pymol command line:
spectrum
In a next step we enabled the the visualization of the cell with this command:
show cell
In order to remove the tumbeling and wiggeling motion of our protein we used the command intra_fit since we are only interested in the internal motions of the protein:
intra_fit protein
The results of these actions can be seen in figure 1 and 2. Figure one shows our WT protein in line view which makes it able to see the motion of the side chains. Figure to shows the protein in cartoon view to see the overall movement of the secondary structure elements.
QUALITY ASSURANCE
CONVERGENCE OF ENERGY TERMS
In this part of quality assurance we analyzed different metrics of our MD simulation by creating plots from our *.edr file. We created plots for the temperature, pressure, energy, volume, density, box, coulomb and van der waals values of our MD simulation by using the tool g_energy as follows:
//calculating temperature enter then "12 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/temperature.xvg
//calculating pressure enter then "13 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/pressure.xvg
//calculating energy (potential, kinetic and total) enter then "9\n10\n11 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/energy.xvg
//calculating volume enter then "18 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/volume.xvg
//calculating density enter then "19 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/density.xvg
//calculating box enter then "15\n16\n17 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/box.xvg
//calculating coulomb enter then "48\n50 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/coulomb-inter.xvg
//calculating van der waals enter then "49\n51 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/vanderwaals-inter.xvg
Temperature Over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Temperature" | 297.886 | 0.007 | 1.57824 | "-0.0105059 (K)" |
In figure 3 we can see that the temperature stays quite the same over the whole simulation which might be interpreted as that our system has reached its stable temperature for simulation.
Pressure over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Pressure" | 1.02313 | 0.023 | 133.659 | "-0.0928554 (bar)" |
Energy over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Potential" | -457312 | 61 | 640.502 | " -423.792 (kJ/mol)" |
| "Kinetic En." | 81855.1 | 1.9 | 433.677 | " -2.88684 (kJ/mol)" |
| "Total Energy" | -375457 | 61 | 784.246 | " -426.678 (kJ/mol)" |
Volume over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Volume" | 356.629 | 0.041 | 0.397685 | " -0.151337 (nm^3)" |
Density over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Density" | 1021.28 | 0.12 | 1.13884 | "0.433467 (kg/m^3)" |
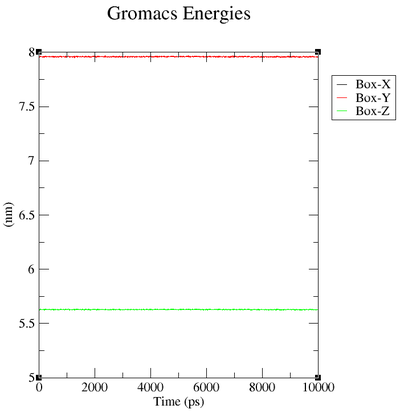
Box over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Box-X" | 7.95996 | " 0.0003" | 0.00295875 | "-0.00112603 (nm)" |
| "Box-Y" | 7.95996 | " 0.0003" | 0.00295875 | "-0.00112603 (nm)" |
| "Box-Z" | 5.62854 | 0.00021 | 0.00209216 | "-0.000796226 (nm)" |
Coulomb over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Coul-SR:Protein-non-Protein" | " -20429.9" | "110" | "425.888" | "-561.713 (kJ/mol)" |
| "Coul-14:Protein-non-Protein" | " 0" | " 0" | " 0" | " 0 (kJ/mol)" |
Van der Waals over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "LJ-SR:Protein-non-Protein" | "-2172.28" | "15" | "136.956" | "-103.12 (kJ/mol)" |
| "LJ-14:Protein-non-Protein" | " 0" | " 0" | " 0" | " 0 (kJ/mol)" |
Questions
1. What is the average temperature and what is the heat capacity of the system?
The average temperature of our system is 297.886 K and the heat capacity ranges from 303 to 292. (values taken from figure 3).
2. What are the terms plotted in the files energy.xvg and box.xvg
In energy.xvg we plot the energy values of kinetic energy, potential energy and total energy over the time of our simulation.
In box.xvg we plot the size of the box around our protein which is given in nm.
3. Estimate the plateau values for the pressure, the volume and the density.
We consider the plateau value as two values, the upper and lower plateau. These plateaus represent the maximum and minimum values of our given plots.
Pressure:
- upper plateau:450 bar
- lower plateau: -450 bar
Volume:
- upper plateau: 357.9 nm^3
- lower plateau: 355.8 nm^3
Density:
- upper plateau: 1026 kg/m^3
- lower plateau: 1017 kg/m^3
4. What are the terms plotted in the files coulomb-inter.xvg and vanderwaals-inter.xvg
The coloumb and van der waals energys of our WT over time.
MINIMUM DISTANCES BETWEEN PERIODIC IMAGES
We ran gromacs with the following command:
//when asked for group selection we selected group 1
g_mindist -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -od /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/minimal-periodic-distance.xvg -pi
And produced the plot seen in figure 11.
In a next step we produced a plot which only uses the C-alpha atoms to calculate the minimum distance between periodic images. For this we used the same command as before. Although, we selected group 3 this time. The result can be seen in figure 12.
Questions
What was the minimal distance between periodic images and at what time did that occur?
The shortest periodic distance is 1.73442 (nm) at time 2720 (ps), between atoms 563 and 5314.
What happens if the minimal distance becomes shorter than the cut-off distance used for electrostatic interactions? Is it the case in your simulations?
If the distance would become shorter than the cut-off distance used for electrostatic interactions our energy would dramatically increase. This did not happen for our simulation so we can assume that our measured value of 1.73 nm is still higher than the cutoff.
Run now g_mindist on the C-alpha group, does it change the results? What does is mean for your system?
With C-alpha group we got a shortest periodic distance of 2.4249 (nm) at time 6805 (ps), between atoms 589 and 5297. This is an increase of the distance since we only consider C-alpha atoms and no side chains as in our previous calculation.
ROOT MEAN SQUARE FLUCTUATIONS
In this part of the analysis we are going to have a look at the root mean square fluctuations. By analyzing this value for our structure we might be able to figure out which parts of our protein are more flexible than others.
To do so we executed the following command:
g_rmsf -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsf-per-residue.xvg -ox /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/average.pdb -oq /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/bfactors.pdb -res
Which gives us three result files:
- rmsf-per-residue.xvg : this file contains a plot over the whole structure length of the RMSF values
- average.pdb : is the average conformation of the structure
- bfactors.pdb: assigned b factor values to the residues which gives us information about the flexibility
Questions
Indicate the start and end residue for the most flexible regions and the maximum amplitudes.
The most flexible region in our structure is from position 131 to 152 which is a loop connecting two alpha-helices. This can be observed in the plot in figure 13 as well as in the 3D view of our protein in figure 14. In general we can say that most of the parts are rather rigid, especially the residues which are located within the core. We observe slightly more flexibility in some alpha-helices which are located at the surface of the protein. Such as the residues located at position 197, 208, 215 and 216. There are also some beta-sheets which contain slightly flexible residues such as residues at position 413 and 420.