Normal mode analysis TSD
The journal for this task can be found here.
Contents
Introduction
For this task 2gk1 is chosen as reference structure since it contains a ligand similar to the native one and therefore allows to easily observe the effect the presence of the ligand exerts on the normal modes. If not otherwise noted, the focus will be on low-frequency modes, since they are thought to play the most important roles in protein conformational changes <ref name=lowfreq1>Delarue,M. and Dumas,P. (2004) On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proceedings of the National Academy of Sciences of the United States of America, 101, 6957-62.</ref><ref name=lowfreq2>Chou,K.C. (1983) Identification of low-frequency modes in protein molecules. The Biochemical journal, 215, 465-9.</ref>.
The alpha subunit of Hexosaminidase A consists of two domains, which are annoated almost equally in Pfam (first domain from 35-165), SCOP (23-166) and CATH (23-164) and will therefore not be separately evaluated for each annotation.
Elastic network models
WEBnm
WEBnm@ is a webserver application with the means of providing a simple and automated computation of low frequency normal modes of proteins. This analysis offers an opportunity to ascertain whether a protein undergoes large amplitude movements and thus is predestined for a more thorough analysis.
Calculations are performed using the C-alpha force field where only the Calpha atoms are considered which are assigned the according whole residue masses. A coarse-grained model is employed and frequencies and energies are interpreted on relative scales and thereforereported without units.
Provided are: deformation energies of each mode, eigenvalues, calculation of normalized squared atomic displacements, calculation of normalized squared fluctuations, interactive visualization of the modes using vector field representation or vibrations and the correlation matrix.
For comparison of dynamics of related protein, the web server additionally features comparative analyses of protein structures<ref name=webnam>http://apps.cbu.uib.no/webnma/about</ref>.
What information do the different servers provide?
Normal modes
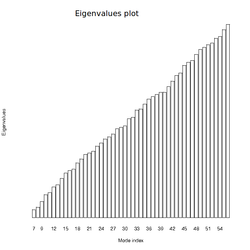
The normal mode analysis was conducted with the 2gk1 chain A with ligand, without ligand and also with the ligand HETATM changed to ATOM. All resulted in the same identical output. It seems the NGT ligand has no effect on the mode calculation. The deformation energies are displayed in <xr id="tbl:denerg"/> and the eigenvalues in <xr id="eigenvalues"/>. Deformation energies and eigenvalues reflect the energy associated with each mode and are inversely related to the amplitude of the motion. That means the lower the eigenvalue and deformation energy the lower also the frequency and mode number but more importantly the larger and more global the motion. Thus the low numbered modes have a lot of rigid regions whereas the modes with higher numbers should show more distributed and intricate motions. Altogether there are 20 modes calculated of which the first 6 are reported in more detail.
<figure id="eigenvalues">
</figure>
<figtable id="tbl:denerg">
| Mode index | Deformation energy | Mode index | Deformation energy |
|---|---|---|---|
| 7 | 1026.72 | 14 | 5215.95 |
| 8 | 1309.04 | 15 | 5670.51 |
| 9 | 1746.16 | 16 | 6228.25 |
| 10 | 2851.91 | 17 | 5862.75 |
| 11 | 3074.36 | 18 | 6990.63 |
| 12 | 3970.00 | 19 | 7653.27 |
| 13 | 3945.10 | 20 | 7962.67 |
</figtable>
<figure id="webnma_correlation">
</figure>
The correlation of all residue movements can be viewed in <xr id="webnma_correlation"/>. There are a lot of red regions alway in the same distance to the diagonal. This shows a high correlation of the corresponding residues. Blue regions show anti-correlation. Interestingly most residues stand in some relation to each other as there are more colored than white regions in the matrix.
<figtable id="tbl:fluct">
</figtable>
The fluctuations of the modes are shown in <xr id="tbl:fluct"/>. The highest displacement shows a loop in the middle of sequence. Further more there is a clear distinction between loops and ends of structural elements that show increased fluctuations and regions with a solid secondary structure that show no variation.
<xr id="tbl:2gk1a_webnma"/> shows all modes with their corresponding deformation energies and atomic displacements. All modes differ in their displacement plots as well as the distinct motions. Mode 7 exhibits a hinge movement with many parts of the protein staying rigid. Mode 8 has more motile protein ends that move in contrary directions to the rest of the protein. In mode 9 the right and left end of the protein twist even further in opposite directions to each other. In mode 10 the loop on the left of the protein that was identified to have a lot of displacement in <xr id="tbl:fluct"/> develops a life of its own where as the rest of the protein stays comparably still. From mode 11 on the protein rotates around its own axis but besides there are no more larger parts moving independently but rather small parts that vibrate.
The domains can be distinguished best in mode 8 and 9 where they move like a hinge against each other. Modes 11 and 12 on the contrary are to rigid in they y-axis as to show signs of separate domains.
The
<figtable id="tbl:2gk1a_webnma">
| Mode | Deformation energy | Visualisation | Atomic displacement |
|---|---|---|---|
| 7 | 1026.72 | ||
| 8 | 1309.04 | ||
| 9 | 1746.16 | ||
| 10 | 2851.91 | ||
| 11 | 3074.36 | ||
| 12 | 3970.00 |
</figtable>
How are the normal modes calculated, that is from which part of the structure? How many normal modes could in principle be calculated for your protein without any cutoff. Visualize the modes (provided by server or using for example PyMol or VMD) and describe what movements you observe: hinge-movement, “breathing”… Which regions of your protein are most flexible, most stable? Can you identify domains for your protein? Compare to the CATH, SCOP and Pfam domains of your protein. For WEBnm@ try the amplitude scaling and vectors option. Try the comparison/upload of second structure option, if: (i) you have PDB structures in different conformations or (ii) your protein has a bound ligand. Then either upload a structure with and one without the ligand, or delete the ligand in your structure. Note: Due to the force field that considers only C_alpha atoms, only changes in the backbone will give results. The model does not resolve changes in side-chain positions or SNPs.
elNemo
elNemo is available only as a webserver and employs elastic network models <ref name=elnemo>Suhre,K. and Sanejouand,Y.-H. (2004) ElNemo: a normal mode web server for protein movement analysis and the generation of templates for molecular replacement. Nucleic acids research, 32, W610-4.</ref>. Atoms considered are limitied to only C-alpha atoms and using a technique termed 'rotation-translation-block', which groups residues into so-called super-residues, there are hardly any restrictions on the input protein's size. The latter approximation is reported to have only little effect on low frequency modes, and the number of residues grouped together is chosen depending on the protein's size. Therefore, small proteins may only contain one residue per super-residue.
Various measurements are reported as results. For each mode, a collectivity can be calculated that expresses how many atoms are affect by the motion of the mode. The larger the value the more atoms are significantly affected.
Additionally, B-factors are calculated from the first 100 normal modes and scaled to the observed values, reported in the PDB file. From this a global correlation value is calculated which describes how well the modes approximate the general global flexibility of the input structure.
For any given mode there is also a map of distance fluctuations created that shows the movement of each residue during the movement of the mode. For this calculation the two most extreme conformations in the mode are used.
Furthermore, the mean square displacement, describing the distance travelled by an atom, is calculated for every C-alpha atom in a mode. This different from the distance fluctuations before, since here, for every time step, the absolute distances are summed up, resulting in the actual distance travelled, which is a different type of information <ref name=msd1> Weisstein, Eric W. "Mean Square Displacement." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/MeanSquareDisplacement.html</ref> <ref name=msd2>http://isaacs.sourceforge.net/phys/msd.html</ref>.
Finally there is a feature still termed experimental, that shows the distance variation between successive residues, again using the two most extreme conformations for the current mode. These values are shown per-residue and should therefore allow one to point out residue pairs that seem to play an important role in mediating the movement of the mode.
Normal Modes
How are the normal modes calculated, that is from which part of the structure? How many normal modes could in principle be calculated for your protein without any cutoff. describe what movements you observe: hinge-movement, “breathing”… Which regions of your protein are most flexible, most stable? Try the comparison/upload of second structure option, if: (i) you have PDB structures in different conformations or (ii) your protein has a bound ligand. Then either upload a structure with and one without the ligand, or delete the ligand in your structure. Note: Due to the force field that considers only C_alpha atoms, only changes in the backbone will give results. The model does not resolve changes in side-chain positions or SNPs.
2gk1:A without NGT
<figtable id="tbl:2gk1a_nongt_elnemo_intro">
| Mode | Frequency | Collectivity | Visualisation | Distance fluctuation | Mean squared displacement |
|---|---|---|---|---|---|
| 7 | 1.0 | 0.49 | |||
| 8 | 1.1 | 0.54 | |||
| 9 | 1.29 | 0.53 | |||
| 10 | 1.66 | 0.39 | |||
| 11 | 1.73 | 0.30 |
</figtable>
The five lowest-frequency modes found by elNemo are shown in <xr id="tbl:2gk1a_nongt_elnemo_intro"/>. As can be seen from the collectivity values, more atoms are significantly affected by the movement in modes 7,8 and 9, than in modes 10 and 11. This is only a crude measurement, however it should be pointed out that the median collectivity among the first 100 modes is xxx, therefore collectivity and frequency seem to NOT? correlate. TODO
TODO which type of movement, b-factor correlation, collectivity
Considering the distinction of the two domains (highlighted in different colors), they are most apparent in mode 8 and to some degree in modes 9 and 10. On the other hand, judging from the motion alone, they would be very hard to spot in mode 7. It is generally evident, that the two alpha-helices of the second domain that are situated towards the face of the first domain, remain comparably flexible. This is visible, especially in mode 8 where both are significantly stretched in a spring-like motion. Furthermore concerning the distinction of the two domains, the previous findings are also found in the distance fluctuation maps which show the most evident distinction in the map of mode 8 while two domains are essent
Generally, the first domain retains a very rigid structure, in all modes but 11. It should be noted however, that the lack of movement within this domain might be attributed to the unresolved region between residues 74 and 89. Other stable structures are most of the alpha-helices in the second domain, with the exception of the two at the binding face, already mentioned above. The central beta-barrel undergoes movement in every mode, however never by a large distance. How the movement of this region might affect binding strength of the ligand remains to be analysed later on. In total the protein shows far less movement than many of the other group's disease's proteins.
Analysing the mean square displacement of all C-alpha atoms also gives some additional insight. The first thing that becomes apparent is that every single mode contains a peak in the middle of the plot, corresponding to resides around SER281 in the original PDB file. Indeed the mode animations show that this loop region at the very left of the figures, exhibits strong movement in every node observed. The movement is even in a somewhat similar fashion in modes 8,9 and 10. An initial idea that comes to mind is that this loop somehow mediates binding to the beta-subunit, however the binding interface of the two subunits forming the catalytically active Hexosaminidase A dimer is far from the loop in question. Instead it seems to be protruding into free space. The strong movement could therefore either be an artefact or fulfilling some function that is not apparent from the data obtained so far. It should be noted that the loop also has a high B-factor in the original resolved structure, therefore contributing positively towards the afore mentioned B-factor correlation value.
In addition, one can also observe that the first domain shows an above average, mean square displacement in all modes, but 11. This is interesting, as it was not immediately apparent from only the animations and this first domain is not the one that contain the catalytic site or any of the residues previously considered important for the enzymes function. It neither seems to be essential for dimer formation. Genereally there seems to be hardly any information on the function of this domain. Another possibility might be that it mediates binding to the GM2 activator protein, which is essential for catalytic activity. However the where on Hex A the activator protein binds also seems to be unknown.
Finally, a region that shows almost no movement in all of the plots is the beginning of the second domain. This can likely be explained that there is only a short loop region that is preceded by a beta-strand participating in a large beta-sheet and followed by a beta-strand that is part of the central beta-barrel of the second domain. Therefore there seems to be little room left for movement without introducing major changes in the whole structure.
2gk1:A with NGT
asdas
Comparison
Can you observe notable differences between the normal modes calculated by the different servers?
Comparison to Molecular Dynamics
When your MD simulations are finished, compare the lowest-frequency normal modes with your MD simulation using visualization software, e.g. PyMol or VMD. Can you observe different movements or similar dynamics? If possible, compare an overlay of the lowest-frequency modes to your MD simulation. You can superimpose the normal modes for example in VMD. What are the advantages and disadvantages of NMA compared to MD?
Conclusion
References
<references/>