Normal mode analysis HEXA
Contents
Webnma
General information
The WEBnma (Webtool for Normal Mode Analysis) is a webtool which allows the user to run a normal mode analysis of its protein. It is public available [here].
This tool offers two different analysis modes (single analysis and comparative analysis). We used the single analysis mode. Therefore, we upload our PDB file, but it is also possible to paste only the PDB id of the protein. Furthermore, it is possible to declare which chain of the protein should be analysed. We pasted our e-mail adress and used the standard parameter for the analysis.
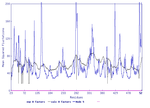
As a result we got a plot with normalized squared atomic displacments for each model. Furthermore, we got pictures of the motion of the protein, which can be seen in the result section.
Results
We analysed the five models with the lowest energy values. Webnma calculates fourteen different models with following energy values:
| Mode Index | Deformation Energy |
| 7 | 1041.88 |
| 8 | 1318.21 |
| 9 | 1738.30 |
| 10 | 2841.31 |
| 11 | 3135.09 |
| 12 | 4100.18 |
| 13 | 3911.06 |
| 14 | 5337.50 |
| 15 | 5741.69 |
| 16 | 6513.85 |
| 17 | 6081.05 |
| 18 | 6882.96 |
| 19 | 7514.14 |
| 20 | 7943.67 |
We took the first five models (7, 8, 9, 10, 11), because they have the lowest energy of all models.
Here you can see the normalized squared atomic displacments of our models:
| model 7 | model 8 | model 9 | model 10 | model 11 |
Here you can see the motion of our analyses.
| model 7 | model 8 | model 9 | model 10 | model 11 |
Discussion
If we look at the squared atomic displacments of our models we can see that almost every model has a peak at the same place.
Here is an overwiew, where are the peaks of the models:
| model 7 | model 8 | model 9 | model 10 | model 11 | |||||
| position of the peak | value of the peak | position of the peak | value of the peak | position of the peak | value of the peak | position of the peak | value of the peak | position of the peak | value of the peak |
| 250 | 3.0 | 10 | 0.8 | 10 | 0.7 | 250 | 8 | 20 | 0.6 |
| 290 | 1.5 | 12 | 0.8 | 15 | 0.7 | 220 | 0.8 | ||
| 300 | 1.5 | 60 | 1.3 | 50 | 0.8 | 310 | 0.9 | ||
| 310 | 1.5 | 90 | 1.0 | 110 | 1.8 | 315 | 0.9 | ||
| 110 | 0.6 | 190 | 0.6 | 350-380 | ~1.2 | ||||
| 115 | 0.6 | 250 | 0.7 | 405 | 1.5 | ||||
| 250 | 2.0 | 310 | 1.2 | 500 | 0.9 | ||||
| 300 | 1.0 | ||||||||
As listed in the table above, each model has a different amount of peaks and also the values differ extremly. Therefore, if you look at the plots (Figure 1 to 5) you have to keep in mind, that the axis are not equal in each model. In out case, model 8 (Figure 2) has the most peaks, whereas model 10 (Figure 4) has only one peak, but this peak has the highest value of the peaks in the models.
Model 7 (Figure 1) has four points in the structure where the peak is very high. These points are located near to each other, which means that there is a very flexible region in the protein. If we look at Figure 6 which presents the motion of model 7 we can see that the highest helix is very flexible, which is probably the region in the protein where the peaks are very high. The rest of the protein moves, because of the hugh movement of this helix.
Model 8 (Figure 2) contains a lot of flexible regions, which are not located next to each other. Therefore, the protein moves at different locations. This means, that there are several independent movements and not only one motion which forces the rest of the protein to move. If we have a look at the visualization in Figure 7, we can see that there are some regions which move indenpently, like the two helices on the right botton or the highest helix, which move from right to left and back.
Model 9 (Figure 3) has also a lot of peaks in the plot. The peaks are very similar to the one of model 8, which means these two models should move in a very similar way. This is the case, as can be seen in Figure 8. Model 9 displays lower movement, than model 8, but the direction of the movement and the regions are the same. The reason therefore is that model 8 has some additional regions which are flexbile.
Model 10 (Figure 4) has only one very high peak at the region around residue 250. By a look at Figure 9 it can be seen that the highest helix shows an extensive movement, which force the rest of the protein to move with it. This motion is similar to the one of model 7, but more concentrated on the helix at residue 250.
The last model, model 11 (Figure 5) displays a lot of peaks as well and one extremly flexible region. The protein moves around the ring which is shown in Figure 10. The complete protein wobble around this ring, which is a similar to the movement of model 8, but here this movement is more pronounced.
In general, all models show relatively similar movements. Especially, the helices at the bottom right and at the top are very flexible, which is consistent in each model.
The Normal mode analysis is just a coarse approximation of the movememnt of the protein. But we think that it is pretty sure, that these three helices are really flexible, because this is the consensus of all different models. Therefore, we suggest, that the protein wobbles around the ring with movements of these helices.
Back to [Tay-Sachs Disease]
El Nemo
General information
ELNemo is a Webinterface to compute Normal Modes by using The Elastic Network Model. The Webserver is available [here].
As input we uploaded our PDB file. Optional it is possible to assign a job name. We changed the parameters according to the task description.
As output we got a fluctuation matrix for each model and also three different pictures of the protein motions from different perspectives.
Results
Here you can see the CA distance fluctuations for the different modes:
This matrix displays the maximum distance fluctuations between all pairs of CA atoms and between the two extreme conformations that were computed for this mode (DQMIN/DQMAX). Distance increases are plotted in blue and decreases in red for the strongest 10% of the residue pair distance changes. Every pixel corresponds to a single residue. Grey lines are drawn every 10 residues, yellow lines every 100 residues (counting from the upper left corner).
| model 7 | model 8 | model 9 | model 10 | model 11 |
El Nemo provides three different animated gif to the user, which show the motions of the protein. Furthermore, we created another animated gif. Therefore, we received four different anmiated gifs which we listed in one line for one model.
Model 7:
| picture from us | picture 1 from ElNemo | picture 2 from ElNemo | picture 3 from ElNemo |
Model 8:
| picture from us | picture 1 from ElNemo | picture 2 from ElNemo | picture 3 from ElNemo |
Model 9:
| picture from us | picture 1 from ElNemo | picture 2 from ElNemo | picture 3 from ElNemo |
Model 10:
| picture from us | picture 1 from ElNemo | picture 2 from ElNemo | picture 3 from ElNemo |
Model 11:
| picture from us | picture 1 from ElNemo | picture 2 from ElNemo | picture 3 from ElNemo |
Discussion
This method provides a fluctation matrix and also some pictures of the motion. The fluctation matrix visualize if two residues come closer together (red) or are more distant (blue) during the motion. So it is possible, to see which residue of the protein behaves in which way.
Furthermore, we got some pictures of the motion in different perspectives, which it made easy to get an imagination of how the protein moves.
The first model (model 7) has almost the same amount of residues that come closer together and which are more distinct. If we have a look at the pictures in Figure 16, we can see, that the whole protein moves. In the first perspective of ELNemo (Figure 16) we can see, that the protein pulsates. Especially one helix shows an up and down movement, which cause the rest of the protein motion. Only the ring in the middle of the protein is relativly stable and shows only low motion.
The second model (model 8) has a different fluctation matrix (Figure 12). At the beginning of the protein the residues are more distant, whereas, at the end of the protein the residues come closer together. In the pictures (Figure 20-23) we can see that, like before, the upper helix shows a strong motion. Furthermore, the lower sheets show stronger motion as well like in the model before. In general this model shows higher motion than the one before. This can be seen for example at the ring, which moves clearly more than the ring from model 7. Again, like before, the protein seems to pulsate.
Although the fluctation matrix of model 9 (Figure 13) is different to the one of model 8, the motion seems to be very equal. In the matrix it can be seen, that the residues just come closer together. There are almost no residues, which get a greater distance to the residues than the one in their QMIN state. Looking at the pictures (Figure 24-27) it can be seen that the motion of model 9 and model 8 is quite similar. Model 9 only shows a bit less motion in the first helix, but the general movement ist equal. Here again, the protein seems to pulsate around the ring.
In model 10 almost all residues come closer together or keep their distance. This matrix (Figure 14) is really different to the other matrices before. Therefore, we suggest, that the protein motion is different to the already discussed models. By a look at the pictures (Figure 28-31) we can see that this assumption is correct. The protein shows a more complex motion than the models before. The protein still contains the movement of the helix at the top, but this motion is very small. Otherwise, the complete protein puslate, but the pulsation is more distinct than before. The whole protein seems to pulste twice, which could not be seen in the other models.
The last model has a fluctation matrix (Figure 15) which is most similar to the one of model 10 (Figure 14). There are less residues which come closer together, but as before, there are no residues which enlarge the distance. So we suggest, that the motion has to be similar to the one of model 10, although the motion should not be so pronounced like by model 10. If we look at the pictures (Figure 32-35), we can see, that this is true. The protein shows less motion and especially the pulsation seems to be low. Only if we look at Figure 33, we can see, that the protein has a hugh pulsation, but the direction is different to the models before.
In general, we can say, that the ring in the middle of the protein is stable and the protein pulsate around them. The different models show different possible occurences of this motion. The top helix is a very flexible one, which has a motion in all different models. Futhermore, each model show pulsation, so we can suggest, that the upper helix moves and the protein pulsate around their center, which is a ring here. All models show similar motions, especially the motion of the upper helix and the lower sheets, which are flexible in each model. So therefore, we can get a coarse imagination of how this protein moves and which parts of the protein are the most important ones for motion.
Back to [Tay-Sachs Disease]
Anisotropic Network Model web server
General information
The Anisotropic Network Model web server can be found [here].
In the web interface, we uploaded our PDB file and chose the chain for which the analysis should be done. Furthermore, we changed the parameters according to the task description.
As an output we received a plot of the real occuring and calculated B-factor values. Furthermore, we got a visualization of motion for each model. Very nice is, that there are arrows in the picture which shows the direction of the motion. So therefore, it is very easy to reconstruct the motion directions.
Results
Here you can see the B-factor distribution of the real occuring B-factors (black) and the calulated B-factors (blue).
| model 1 | model 2 | model 3 | model 4 | model 5 |
The following table displays the motion of protein for the different models:
| model 1 | model 2 | model 3 | model 4 | model 5 |
Discussion
This method provides a distribution of the real occuring B-factors and the calculated B-factors. By comparing both values we can see which parts of the protein are flexible. A high B-factor value means a high flexbility of this residue. If we look at the plots in detail, on the first view all values seem to be very similar. Each model has four very high peaks at the same place, but at the rest of the protein the values differ between the different models. All models have big peaks at the beginning of the protein as well, which was expected, because the beginning and the end of a protein are often very flexbile (therefore, most methods which predict disordered regions predict them at the beginning or the end of the protein).
The first model (Figure 41) has only one loop which shows strong motion and therefore the rest of the protein follows the motion of this loop. It seems that the whole protein contract and strecht. This motion is caused by the motion of the flexible loop.
The second model (Figure 42) shows a complexer motion, with more than one motion center. There are two contrary motions. As before, the loop moves from right to left. But at the other side of the protein, there is a second loop which moves forward and backward as well. These two loops move in the same time to the same direction. Therefore, it seems that the protein build a deeper curve by moving the two loops. The rest of the protein follows the motion of these two loops. Only the ring does not change its structure in a very obvious way.
In the third model (Figure 43) there are again two loops which moves. They are the same loops as before. But this time, the loops move contrary. If one loop moves forward, the other loop moves backward. Therefore, the rest of the protein has not to move as much as in model 2. The ring is again very rigid and does not change its structure.
The forth model (Figure 44) has only one loop which moves. But in this case not only the loop moves, but also the associated helix. This causes a stronger movement of the whole protein, like in model 1. This is the first case where the ring itselfs moves. This causes that the loops, which build the ring, come closer together.
The last model (Figure 45), has three different motions. The two loops from model 2 and 3 moves again. But there is also a helix which moves. Compared to the other models, this model displays the strongest motion and the whole protein seems to be very unstable. The ring shows a lot of motion as well.
In general there are two parts of the protein which seem to be the center of motion in almost all models. The last model is very unstable and therefore, we do not suggest that this is the real motion of the protein. We suggest, that especially the two loops are the center of motion and the rest of the protein follows this motion. It was not possible to decide if both loops moves in the same or in contrary directions, because these models are just coarse approximations of the protein motion and both cases could be the real motion. To sum up, we suggest, that the protein has two loops which act as motion center. Besides, the ring does not move that much and keeps its structure while the rest of the protein follows the motion of the two motion centers.
Back to [Tay-Sachs Disease]
oGNM – Gaussian network model
General information
The Gaussian network model (oGNM) web server can be found [here].
The oGNM is an online server which can calculate the essential dynamics of PDB structures and of user-modified or unrealised structures. The method is based on an Elastic Network (EN) model called the Gaussian Network Model (GNM). The online server was an enlargment of the already existing database iGNM which also uses the GNM and which contains already a lot of PDB structures.
The advantages of the server compared to iGNM or other normal mode analysis tools is that the calculation is very fast and a result is received in a few seconds. Furthermore, it is not limitied in size which means it is not necessary to use really small structures like in other normal mode analysis methods.
For the calculation the method uses a network model that represents the biomolecular structure. This network can be identified by the alpha-carbon atoms and some other selected atoms on nucleotides. Furthermore, they assume that the fluctuations of the nodes are isotropic and Gausian. Therefore, there exist different parameters which can be selected before the calculation: number of model nodes to represent a nucleotide (1 or 3) and the interaction cutoff distance for nucleotide and amino acid pairs (the c-alpha cutoff is the average of this two cutoffs).
The method delivers plenty of different output files, like the Eigenvalues and the Kirchoff matrix which play a role in the calculation of the 20 slowest modes which is part of the results as well. Furthermore, there are three main representive results which displays the fluctuation and the mobility of the structure as well as the cross-correlation plot between the desired modes.
(Sources: [Paper] and [Webserver])
Results
Full diversity of the received output can be seen [here]. For the analysis of the result we decided to display only the three main visualizations.
Here you can see the mobility profiles. This plots can be used for the comparitive analysis of the different mode profiles. On the x-axis are the residues of chain A and the y-axis displays the according fluctuation. The first five pictures display the modes 7-11 on their own and the last picture displays all modes together.
| mode 7 | mode 8 | mode 9 | mode 10 | mode 11 | all modes |
The next picture displays the mobility of the different modes. The mobility goes from blue to red, where blue means little mobility and red means high mobility.
| mode 7 | mode 8 | mode 9 | mode 10 | mode 11 |
Here you can see the cross-correlation plot of mode 7-11. The colors of the plot go from dark red to dark blue whereas dark red colored parts are indicating a positive correlation of motion between the different modes. Contrary the dark blue parts display negative correlated motions.
Discussion
Looking at the mobility profile, one can see that there are two different peeks for the fluctuation that stands out. The first peek is around residue 150. There, the fluctuation jump betwenn 0.2 and 0.7 in different modes. This peek can be seen in mode 7 (Figure 47) and 9 (Figure 49) where it is the only existing peek as well as in mode 8 (Figure 48) and 11 (Figure 51). The other outstanding peek ist the one around residue 525, which can be seen in mode 8, 9 and 10 (Figur 50). There the fluctuation differs between 0.1 and 0.4 in the different modes. The only exception is mode 10 which is the only one which has many different peeks at very low fluctuation level under 0.1. Furthermore, the other modes contain also some other small fluctuation peeks. However, Figure 52 which contains all different fluctuation plots displays also this two outstandig peeks at residue 150 and 525. This indicates that at this two residues the fluctation is probably the highest and that there are some more residues which have a low fluctuation.
The 3D visualization of the chain A of hexosaminidase with the corresponding mobility deliver similar results. Mode 7 (Figure 53), 8 (Figure 54) (rotation here differs a bit which makes it in this case hard to see), 9 (Figure 55) and 11 (Figure 57) show arised mobility in the beta-sheets which are here on the left side. Mode 7, 8 and 11 are more and darker red colored which means there they have a higher mobility. Looking at the only colored part in mode 9 (white) it agrees with the red darkest part in mode 7 and 11. This is similar to the mobility profiles where all this modes have the highest peek at residue 150. Contrary, Mode 8 and 10 (Figure 56) have some other parts which have also higher mobility. In mode 8 part of the helices on the right side have high mobility. In mode 10 most alpha-helices on the right side have high mobility. This agrees also with the mobility profile where mode 10 displays many fluctuations whereas mode 8 has only one peek aroud resiude 525.
Therefore, both the mobility profile as well as the 3D visualization show evidence that there are two parts in chain A which have higher mobility. This two parts are around ther residues 150 and 525. In the 3D-visualization the parts complies with the right and on the left 'ends'.
The cross-correlation plot (Figure 58) displays the correlated motion of the modes 7-11. There are three boxes along the diagonal which are outstanding. This boxes contain regions of dark blue and dark red which means there are positive and negative correlations present. The rest of the correlation plot displays mostly no outstanding correlation. This means that there is no motion correlation of two completly different parts of the structure regarding this different modes. This agrees with the plots and the 3D visualization described above where the motion is consistent between the different modes.
Back to [Tay-Sachs Disease]
NOMAD-Ref
General information
The Normal Mode Analysis, Deformation and Refinment (NOMAD-REF) web server can be found [here].
NOMAD-Ref is an online server which provides tools for the normal mode calculation and algorithms that use normal modes for structural refinement or optimization. The Normal Modes were widley calculated by Elastic Network Model (ENM). Furthermore, there exists the option to use classical force fields for the calculation.
In addition to the Normal Mode calculation which is used as the basis, NOMAD-Ref provides three different possibility for further analysis. The first one is the geration of alternative models with correct stereochemistry but large amplitude movements. The next two are two different kinds of refinements: refinement of the models against experimental data (e.g. X-Ray diffraction) and the refinement ot the docking solutions when the receptor is known flexible.
NOMAD-Ref tools can be applied for all PDB-structures, even for very larg proteins it can include all atoms. For the calculation of the normal mode and following visualization different parameters can be choosen. You can select the number of modes to be calculated, the distance weight parameter (Ångström), the cutoff to use for mode calculation (Ångström) and the average RMSD (Ångström) in output trajectories.
(Source: [website])
Results
The following plots display the cRMS of the different modes. The cRMS displays the strength of the movement according to the atome.
| model 7 | model 8 | model 9 | model 10 | model 11 |
The following Table contains the predicted motions of the model 7-11:
| model 7 | model 8 | model 9 | model 10 | model 11 |
Discussion
The first plots (Figure 59-63) contain the cRMS of the different modes. The cRMS displays the strength of the movement according to the atome. Mode 7, 8 and 10 have an cRMS between 1 and 25 Angstrom. This movements are on the entire length and have some peeks at the beginning, in the middle and at the end. Mode 8 has at the end one outstandig peek which has a very high cRMS at about 25 Angstrom. The rest of the atmos in mode 8 have lower cRMS, like all atoms in mode 7 and 10. This means that mode 8 moves harder at one end.
The other two modes 9 and 11 have one outstandig peek at a very high cRMS at about 250 Angstrom. The rest of the atoms in both modes have a lower cRMS which is equal to the cRMS over all atoms in mode 7, 8 and 10. This follows, that mode 9 and 11 have at one position in the structure a very extrem movement.
A further output of Nomad-Ref were the movies which display the motion and which are shown in Figure 64-68. Here we can see, that mode 7, 8 and 10 have some movement at the ends of this structure. Mode 8 and 10 move very similar and seesaws the ends of the structure up and down. In contrast, mode 7 moves the ends to the back which looks like it folds in structure-center direction. The other two modes 9 and 11 also move the ends of the structure, but contain also a extrem movement. Excluding the extrem one, these two modes also display this up and down seesaw like motion.
The movements of all modes correspond exactly with the above discribed plots and indicate motions at both ends of the structure. The outstandig extrem movement of mode 9 and 11 is in our eyes too strong and probably not realistic. In the most modes the movement of the ends is seesaw like up and down. Therefore, we believe that this can probably be a movement of hexosaminidas chain A.
Back to [Tay-Sachs Disease]
All-atom NMA using Gromacs on the NOMAD-Ref server
General information
The all-atom Gromacs-NMA on the NOMAD-Ref webserver can be found [here].
The all-atome Gromacs-NMA is a normal mode calculation that does not use elastic networks like the other methods provided by Nomad-Ref. In contrast, this method use classical force fields. Therefore, it creates an all-atom topology of the input structure. One disadvantage is that this method takes more time and memory space than the elastic network calculation. Therefore, the size of the structure is limitated to 5000 atoms on the server.
(Source: [website])
Results
For the all-atom NMA we had to use the structure of 1BPT, because chain A of the hexosaminidase was to big. Furthermore, we run the all-atome NMA twice with different temperatures (600K and 2000K).
600K
Here you can see the motion of 1BPT at temperature 600K.
| model 7 | model 8 | model 9 |
2000K
Here you can see the motion of 1BPT at temprature 2000K.
| model 7 | model 8 | model 9 |
Comparison to an Elastic Network Calculation
Next, we want to compare the result of All-atom NMA to the elastic network calculation of NOMAD-Ref.
| model 7 | model 8 | model 9 |
Discussion
Looking at the differenz modes of 1BPT calculatet at 600K (Figure 69-71) and 2000K (Figure 72-74), one can see that there is no big difference. All modes display a see-saw like movement where the right and left loop-like parts move up to the center. They neither show a difference in speed nor in the way of movement. This suggests that the temperature has no high influence on the motion of 1BPT.
Compared to the Nomad-Ref Elascit Network calculation (Figure 75-77) more differenence can be seen. First of all, mode 7 moves completly different. The ends of this mode do not move up to the center. Instead, the ends are more rigid and the whole body moves. The ends in mode 8 and 9 have a stronger motion, where especially the coil region (green) displays more flexibility. Mode 9 has the most powerfull movement at this coil region.
All in all, all modes,except mode 7 of the elastic network calculation, agree. One remarkable thing is that the movement of the elastic network calculation is in somehow more flexibel. Because all modes have this see-saw like movement of the right and left loop-like parts move, we believe that this is probably the real movement of 1BPT.
Back to [Tay-Sachs Disease]
Summary and Comparison of the Methods
The most methods except oGNM deliver a movie of the motion. oGNM displays only the regions in structure where motion is excpected. The other methods deliver a wide range of models. This models are within a method very consistent. This means that the models agree mostly.
Regarding the predicted movements of the different methods, they show similar motions as well. In most methods the most movement exists in the two outstandig parts around the ring in the center. This movements itselfs can differ between methods and models. Furthermore, in some methods the ring displays also some small movements.
Some certain models of one method can also deviate from the rest of the models. Therefore, it is important to look at more than one model. Furthermore, there can also be some unrealistic movements like the one from Nomad-Ref. This is another reason why it is importent to check the movement.
One importent thing ist that all tools work really fast and have no limitation in size. Furthermore, compared to the force field calculation of Nomad-Ref it does not differ too much. This indicates that the normal mode analysis delivers a motion which gives a good overview how the structure will probably move. It can differ in some submotions, but it is mostly a got approximation.
To sum up, normal mode analysis delivers a good approximation for the motion of one structure. It is very fast and is comparable to the force field calculation of Nomad-Ref. Therefore, it enables to get a fast overview of the movement. If you want a detailed and really realistic prediction of the movement it is probably better to make the more complicated Molecular Dynamics calculation.
Back to [Tay-Sachs Disease]
Comparison to Molecular Dynamics
To distinguish the qualitiy of the normal mode analysis we compare the results to the one achieved by molecular dynamics. The following movies display the motion of the subunit alpha of the beta-hexosamindase.
First, we can see that the resulting motions of the normal mode analysis look more flowing and not so mechanic. This movies show mainly the movement of big parts of the protein. Contrary, in molecular dynamics movies display the movement of each single secondary structure in detail. Comparing the resulting movies, we can see that they agree in the fact that the outer parts of the protein move most whereas the center is more rigid. However, the molecular dynamic movement is not a stong movement of the whole region together like in the normal mode analysis movements where this two regions move extrem to the center for example. Contrary, the secondray structure element move strong on their own and not necessary in the same direction together. Afterwards we compare the whole movement of the moldecular dynamics simulation with the normal mode simulation. One problem was that it was not possible to upload the whole motion for the molecular dynamics simulation. Therefore, we only upload the fist part of the simulation. The whole movie of the movement displays a similar behaviour like the one created by normal mode analysis. Tha major difference is that the movement is sparser.
All in all, the molecular dynamic simulation provides a more detail view of the movement which is good for detailed movement analysis. One disadvantage is that it takes much time to create this simulation and a lot of preparatory work is necessary. The normal mode analysis delivers a worse simulation of movement which can disagree in the different modes. However, it is a good approach which can give fast an overview over the movement.