Fabry:Normal mode analysis

Fabry Disease » Normal_mode_analysis

Introduction

<figure id="fig:bindSite">

This figure shows the substrate binding site of the structures 3HG2 (pale blue) and 3HG3 (pale green). In dark blue and dark green we highlighted the residues involved in binding the substrate (residues 203 – 207) α-D-Galactose, which is shown in red.

</figure>

Maybe one of the first questions that can be asked in this task is, why we use low-frequency normal modes. This is explained in the paper of Marc Delarue and Philippe Dumas<ref>Marc Delarue and Philippe Dumas On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models, Proc. Natl. Acad. Sci. (USA), 101, 6957-6962 (2004)</ref>, where they claim, that "many of the structural transitions (...) can be explained by just a few of the lowest-frequency normal modes". The normal modes can be used to generate the general motion of a system by superposition them. Thus we could in principle infer from our analysis in this task how the alpha-galactosidase A, which we examine hydrolyses the terminal alpha-galactosyl moiety of its substrate<ref>Normal mode http://en.wikipedia.org/wiki/Normal_mode, July 5th, 2012</ref>.

We decided to use the structures 3HG2 and 3HG3, which represent the human α-Galactosidase catalytic mechanism with empty active site and substrate bound, respectively (see <xr id="fig:bindSite"/>). From this, we hope to getter an insight into the mechanism and a possibility to compare normal modes and the behaviour of the molecule.

Possible normal modes:
The structure 3HG2 has 781 C-alpha atoms in its pdb file, thus 781*3 - 6 = 2337 normal modes could be calculated in principle for this structure without any cutoff by elNémo. Since the structure has a total of 6765 atoms, 20289 NMs could be calculated by WEBnm@.
The structure 3HG3 has 793 C-alpha atoms in its pdb file, thus 793*3 - 6 = 2373 normal modes could be calculated in principle for this structure without any cutoff by elNémo. Since the structure has a total of 7537 atoms, 22605 NMs could be calculated by WEBnm@.

WEBnm@

WEBnm@ <ref>Hollup SM, Sælensminde G, Reuter N. WEBnm@: a web application for normal mode analysis of proteins BMC Bioinformatics. 2005 Mar 11;6(1):52 </ref> claim to administer simple and automated computation of low-frequency normal modes for proteins as well as their analysis in order to clarify if it is beneficial to perform a complete study on the protein in question.
The server calculates Normal Modes with the help of the MMTK package <ref>Hinsen K, The Molecular Modelling Toolkit: a new approach to molecular simulations, J Comput Chem, 21:79-85, 2000</ref>, which is an Open Source program library for molecular simulation applications. A C-alpha force field <ref>Hinsen K, Petrescu AJ, Dellerue S, Bellissent-Funel MC, Kneller GR, Harmonicity in slow protein dynamics, Chemical Physics, 261:25-37, 2000</ref> is used and only these C-alpha atoms are used, but with a weight assigned that corresponds to the masses of the whole residue they represent.
The server provides a bunch of analysis tools and all results can be downloaded without any problems. The tools are:

• deformation energies of each mode
• eigenvalues
• calculation of normalized squared atomic displacements
• calculation of normalized squared fluctuations
• interactive visualization of the modes using vector field representation or vibrations
• correlation matrix

Deformation energies and eigenvalues

<figure id="fig:eigen3HG2">

Shown are the Eigenvalues for each mode from 7 to 57 from the structure 3HG2. Except for a jump between mode 16 and 17 the increase is almost linear.

</figure> <figure id="fig:eigen3HG3">

Shown are the Eigenvalues for each mode from 7 to 57 from the structure 3HG2. Due to several jumps in the values, the increase is not really linearly.

</figure>

In <xr id="fig:eigen3HG2"/> and <xr id="fig:eigen3HG3"/> the Eigenvalues for the first 50 modes for both examined structures are plotted. The increase of the values shows a decrease of amplitude of motion in the modes, since there is an invers relationship between the Eigenvalues and the amplitude. Hence, mode 7 has the highest amplitude.

<figtable id="tab:DeformationEnergies"> Deformation Energies 3HG2 and 3HG3 as calculated by WEBnm@

Mode Index	Deformation Energy 3HG2	Deformation Energy 3HG3
7	406.07	318.52
8	580.11	508.88
9	1062.04	1078.20
10	1703.56	1621.95
11	1808.92	1827.08
12	2227.10	2019.97
13	2541.59	2481.89
14	3109.43	2695.35
15	3345.86	3321.12
16	3842.69	3588.18
17	4868.07	3782.94
18	5178.29	4404.61
19	6119.79	5349.94
20	5940.89	6027.59

</figtable>

Mode Visualization

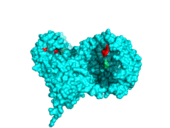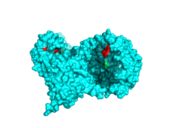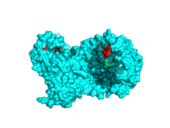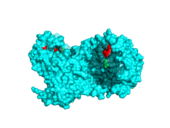
<figtable id="tab:webnma_3hg2"> In this table the 6 modes are shown, that were calculated by WEBnm@. Depicted is the structure 3HG2, which represents the Human α-galactosidase catalytic mechanism with empty active site in cyan and the substrate binding site at position 203 to 207 highlighted in red.

WEBnm@ mode 7 of 3HG2	WEBnm@ mode 8 of 3HG2	WEBnm@ mode 9 of 3HG2
WEBnm@ mode 10 of 3HG2	WEBnm@ mode 11 of 3HG2	WEBnm@ mode 12 of 3HG2

</figtable>

<figtable id="tab:webnma_3hg3"> In this table the 6 modes are shown, that were calculated by WEBnm@. Depicted is the structure 3HG3, which represents the Human α-galactosidase catalytic mechanism with bound substrate (green, α-D-Galactose with bound α-D-Glucose) in cyan and the substrate binding site at position 203 to 207 highlighted in red.

WEBnm@ mode 7 of 3HG3	WEBnm@ mode 8 of 3HG3	WEBnm@ mode 9 of 3HG3
WEBnm@ mode 10 of 3HG3	WEBnm@ mode 11 of 3HG3	WEBnm@ mode 12 of 3HG3

</figtable>

Average Energies

<figure id="fig:avEn">

...

</figure> <figtable id="tab:AverageEnergies"> Average energies for mode 7 to 20, calculated by WEBnm@ for the structures 3HG2 and 3HG3

Mode Index	3HG2	3HG3
7	406.07	318.52
8	580.11	508.88
9	1062.04	1078.2
10	1703.56	1621.95
11	1808.92	1827.08
12	2227.1	2019.97
13	2541.59	2481.89
14	3109.43	2695.35
15	3345.86	3321.12
16	3842.69	3588.18
17	4868.07	3782.94
18	5178.29	4404.61
19	6119.79	5349.94
20	5940.89	6027.59

</figtable>

Motion

Atomic Displacement Analysis

<figure id="fig:atomDisplacement3HG2">

This figure displays the normalized square of the atomic displacements of the C alphas of the structure 3HG2 for the modes 7 to 12 calculated by WEBnm@. This molecule is a homodimer and hence both chains are shown - chain A in green, chain B in blue. Position 1 through 31 are skipped, since they form the signal peptide and are cleaved.

</figure>

<figure id="fig:atomDisplacement3HG3">

This figure displays the normalized square of the atomic displacements of the C alphas of the structure 3HG3 for the modes 7 to 12 calculated by WEBnm@. This molecule is a homodimer and hence both chains are shown - chain A in green, chain B in blue. Position 1 through 31 are skipped, since they form the signal peptide and are cleaved.

</figure>

In <xr id="fig:atomDisplacement3HG2"/> and <xr id="fig:atomDisplacement3HG3"/> the square of the atomic displacements of the C alphas of the examined structures are shown. These are normalized in a way, such that the sum over all residues is equal to 100. With these plots we can find out, which regions are displaced most, i.e. which move the most; this is shown by the highest values. It is recommended to look for clustered peaks, which identify significantly big regions. Local flexibility (a single peak) is of less importance.

In both figures, chain A and B are colored different. From this we can see, that although in <xr id="tab:webnma_3hg2"/> and <xr id="tab:webnma_3hg3"/> the motion of both chains in a mode looks alike, but in general it is not perfectly equal or even differs a lot. A good example for a significant variation is mode 7 of the structure 3HG2 (see <xr id="fig:atomDisplacement3HG2"/>, upper left). While the first part of both chains (approximately until position 200) behaves similiar, except for a different amplitude, the second half differs with chain B showing much more movement. This action can be oberserved in <xr id="tab:webnma_3hg2"/> only after a very close inspection.
For the dimer it seems to be easier to act different when no substrate is bound, since the atomic displacements of the chains in the modes of 3HG3 seem to be much more alike than those of 3HG2.

All in all, the substrate binding site itself (residue 203 to 207) seems to be rather ridgid, except for maybe mode 10 in 3HG3, while the ends of both chains (the last 50 residues) are fairly flexible. This can best be seen in both modes 12.

Fluctuations

<figure id="fig:fluctuation_3HG2">

Here the normalized square of the fluctuation of each Calpha atom (for all non-trivial modes) for the structure 3HG2 is shown. This molecule is a homodimer and hence both chains are shown - chain A in green, chain B in blue. Position 1 through 31 are skipped, since they form the signal peptide and are cleaved. In the left plot, both chains are superimposed to show to which extend they behave alike.

</figure>

<figure id="fig:fluctuation_3HG3">

Here the normalized square of the fluctuation of each Calpha atom (for all non-trivial modes) for the structure 3HG3 is shown. This molecule is a homodimer and hence both chains are shown - chain A in green, chain B in blue. Position 1 through 31 are skipped, since they form the signal peptide and are cleaved. In the left plot, both chains are superimposed to show to which extend they behave alike.

</figure>

Fluctuation is the sum of the atomic displacements of each C alpha atom in each non-trivial mode weighted by the inverse of their corresponding eigenvalues. These are normalized in a way, such that the sum over all residues is equal to 100. The fluctuations of the structures 3HG2 and 3HG3 are shown in <xr id="fig:fluctuation_3HG2"/> and <xr id="fig:fluctuation_3HG3"/>, respectively.

The plots support our previous assumption, that the chains of the substrate bound structure 3HG3 act much more similiar than those of the structure with an empty active site, since the overlap is almost perfect in the left plot of <xr id="fig:fluctuation_3HG3"/>.

Again we can observe that the binding site is an rigid island among two moderate flexible regions, which probably are responsible for opening and closing the binding pocket and the needed movement for the breake down of the bound sugar.
Towards the end of the chain more motion can be observed, which is needed for the independant movement of both chains.

Correlation Matrix

<figure id="fig:corrMatr3HG2_3HG2">

...

</figure> <figure id="fig:corrMatr3HG3_3HG2">

...

</figure>

Plots the correlation of motions between all the Calphas in the protein structure.

Overlap Analysis

General error. A trouble ticket has already been send on 04.07.2012 11:22

ElNémo

B-factor analysis

3HG2: Correlation= 0.651 for 781 C-alpha atoms.
3HG3: Correlation= 0.779 for 793 C-alpha atoms.

Mode Visualization

<figtable id="tab:elnemo_3hg2"> In this table are the 10 modes shown, that were calculated by ElNémo. Depicted is the structure 3HG2, which represents the Human α-galactosidase catalytic mechanism with empty active site in cyan and the substrate binding site at position 203 to 207 highlighted in red.

ElNémo mode 7 of 3HG2	ElNémo mode 8 of 3HG2	ElNémo mode 9 of 3HG2	ElNémo mode 10 of 3HG2	ElNémo mode 11 of 3HG2
ElNémo mode 12 of 3HG2	ElNémo mode 13 of 3HG2	ElNémo mode 14 of 3HG2	ElNémo mode 15 of 3HG2	ElNémo mode 16 of 3HG2

</figtable>

<figtable id="tab:elnemoSURF_3hg3"> In this table are the 10 modes shown, that were calculated by ElNémo. Depicted is the structure 3HG3, which represents the Human α-galactosidase catalytic mechanism with bound substrate (green, α-D-Galactose with bound α-D-Glucose) in cyan and the substrate binding site at position 203 to 207 highlighted in red.

ElNémo mode 7 of 3HG3	ElNémo mode 8 of 3HG3	ElNémo mode 9 of 3HG3	ElNémo mode 10 of 3HG3	ElNémo mode 11 of 3HG3
ElNémo mode 12 of 3HG3	ElNémo mode 13 of 3HG3	ElNémo mode 14 of 3HG3	ElNémo mode 15 of 3HG3	ElNémo mode 16 of 3HG3

</figtable>

Distance variation

<figure id="fig:FABRY_caStrain3HG3">

...

</figure>

<figure id="fig:FABRY_caStrain3HG2">

...

</figure>

This graph displays the distance variation between successive pairs of CA atoms in the two extreme conformations that were computed for this mode (DQMIN/DQMAX). Large distance variations can be an indicator for residue pairs that support the important strain in that particular normal mode movement. Note that residue pairs between chain breaks or at flexible ends of the protein may also exhibit large CA-CA distance variations. If more than one residues ae grouped together into a rigid block (NRBL>1), CA-CA distance variations between CA atoms in the same block will be very low.

This feature is still experimental and will be further developped in the future.

Distance fluctuations

<figtable id="tab:elnemo_fluct_3hg2"> ...

Distance fluctuations of mode 7 (3HG2)	Distance fluctuations of mode 8 (3HG2)	Distance fluctuations of mode 9 (3HG2)	Distance fluctuations of mode 10 (3HG2)	Distance fluctuations of mode 11 (3HG2)
Distance fluctuations of mode 12 (3HG2)	Distance fluctuations of mode 13 (3HG2)	Distance fluctuations of mode 14 (3HG2)	Distance fluctuations of mode 15 (3HG2)	Distance fluctuations of mode 16 (3HG2)

</figtable>

<figtable id="tab:elnemo_fluct_3hg2"> ...

Distance fluctuations of mode 7 (3HG3)	Distance fluctuations of mode 8 (3HG3)	Distance fluctuations of mode 9 (3HG3)	Distance fluctuations of mode 10 (3HG3)	Distance fluctuations of mode 11 (3HG3)
Distance fluctuations of mode 12 (3HG3)	Distance fluctuations of mode 13 (3HG3)	Distance fluctuations of mode 14 (3HG3)	Distance fluctuations of mode 15 (3HG3)	Distance fluctuations of mode 16 (3HG3)

</figtable>

This matrix displays the maximum distance fluctuations between all pairs of CA atoms and between the two extreme conformations that were computed for this mode (DQMIN/DQMAX). Distance increases are plotted in blue and decreases in red for the strongest 10% of the residue pair distance changes. Every pixel corresponds to a single residue. Grey lines are drawn every 10 residues, yellow lines every 100 residues (counting from the upper left corner).

References

<references/>