Difference between revisions of "Task 10: Molecular Dynamics Analysis"
(→HYDROGEN BONDS) |
(→RAMACHANDRAN (PHI/PSI) PLOTS) |
||
| Line 1,118: | Line 1,118: | ||
| [[File:PAH_NATIVE_ramachandran_ARG_408.png | thumb | 300px | Figure 86: Ramachandran plot of the residue 408 in the md simulation of the native.]] |
| [[File:PAH_NATIVE_ramachandran_ARG_408.png | thumb | 300px | Figure 86: Ramachandran plot of the residue 408 in the md simulation of the native.]] |
||
|} |
|} |
||
| + | |||
| + | In the overall ramachandran plot the region around the psi-angle 100 and the phi-angle 200 and the region around the psi-angle 100 and the phi-angle -200 seems to be less populated than in the WT. The residue 408 shows in the WT and in the mutated simulation some outliers, but the main population site is quite the same. |
||
=== ANALYSIS OF DYNAMICS AND TIME-AVERAGED PROPERTIES === |
=== ANALYSIS OF DYNAMICS AND TIME-AVERAGED PROPERTIES === |
||
Revision as of 17:00, 26 September 2011
In this task we are going to analyze the results of the molecular dynamics simulations of task 8. A detailed task description can be found here. The analysis focuses on this tutorial.
Contents
- 1 Native
- 2 P281L
- 3 R408W
Native
A BRIEF CHECK OF RESULTS
In order to verify that our simulation ran successfully we used the command line tool gmxcheck. we executed it as follows for our .xtc file:
gmxcheck -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc
How many frames are in the trajectory file and what is the time resolution?
We observed 2001 frames with a time resolution of 5ps.
How long did the simulation run in real time (hours), what was the simulation speed (ns/day) and how many years would the simulation take to reach a second?
The simulation ran 4h00:39 and had a simulation speed of 59.835 ns/day. To calculate 1 second we would need (1 / (59 * (10^(-9)))) / 365 = 46 436.0344 years
Which contribution to the potential energy accounts for most of the calculations?
- potential energy: -4.57312e+05 kJ/mol
- greatest contribution by Coulomb: -4.46176e+05 kJ/mol
VISUALIZATION OF RESULTS
We extracted 1000 frames from the trajectory (-dt 10), leaving out the water (selected Protein when asked for a selection). Moreover, we will remove the jumps over the boundaries and make a continuous trajectory (-pbc nojump):
trjconv -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -o protein.pdb -pbc nojump -dt 10
After that we opened the generated protein.pdb file with pymol. Here we changed the coloring to spectrum by typing the following to the pymol command line:
spectrum
In a next step we enabled the the visualization of the cell with this command:
show cell
In order to remove the tumbeling and wiggeling motion of our protein we used the command intra_fit since we are only interested in the internal motions of the protein:
intra_fit protein
The results of these actions can be seen in figure 1 and 2. Figure one shows our WT protein in line view which makes it able to see the motion of the side chains. Figure to shows the protein in cartoon view to see the overall movement of the secondary structure elements.
QUALITY ASSURANCE
CONVERGENCE OF ENERGY TERMS
In this part of quality assurance we analyzed different metrics of our MD simulation by creating plots from our *.edr file. We created plots for the temperature, pressure, energy, volume, density, box, coulomb and van der waals values of our MD simulation by using the tool g_energy as follows:
//calculating temperature enter then "12 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/temperature.xvg
//calculating pressure enter then "13 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/pressure.xvg
//calculating energy (potential, kinetic and total) enter then "9\n10\n11 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/energy.xvg
//calculating volume enter then "18 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/volume.xvg
//calculating density enter then "19 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/density.xvg
//calculating box enter then "15\n16\n17 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/box.xvg
//calculating coulomb enter then "48\n50 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/coulomb-inter.xvg
//calculating van der waals enter then "49\n51 0"
g_energy -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.edr -o ../../../Dropbox/Studium/3_semester/master_praktikum/task10/vanderwaals-inter.xvg
Temperature Over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Temperature" | 297.886 | 0.007 | 1.57824 | "-0.0105059 (K)" |
In figure 3 we can see that the temperature stays quite the same over the whole simulation which might be interpreted as that our system has reached its stable temperature for simulation.
Pressure over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Pressure" | 1.02313 | 0.023 | 133.659 | "-0.0928554 (bar)" |
Energy over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Potential" | -457312 | 61 | 640.502 | " -423.792 (kJ/mol)" |
| "Kinetic En." | 81855.1 | 1.9 | 433.677 | " -2.88684 (kJ/mol)" |
| "Total Energy" | -375457 | 61 | 784.246 | " -426.678 (kJ/mol)" |
Volume over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Volume" | 356.629 | 0.041 | 0.397685 | " -0.151337 (nm^3)" |
Density over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Density" | 1021.28 | 0.12 | 1.13884 | "0.433467 (kg/m^3)" |
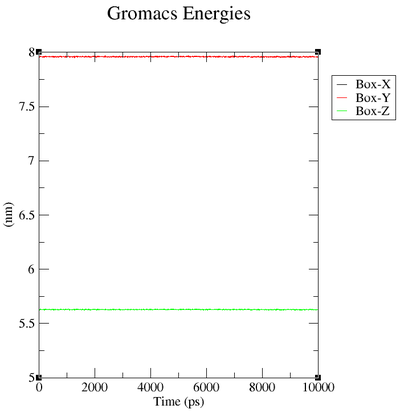
Box over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Box-X" | 7.95996 | " 0.0003" | 0.00295875 | "-0.00112603 (nm)" |
| "Box-Y" | 7.95996 | " 0.0003" | 0.00295875 | "-0.00112603 (nm)" |
| "Box-Z" | 5.62854 | 0.00021 | 0.00209216 | "-0.000796226 (nm)" |
Coulomb over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Coul-SR:Protein-non-Protein" | " -20429.9" | "110" | "425.888" | "-561.713 (kJ/mol)" |
| "Coul-14:Protein-non-Protein" | " 0" | " 0" | " 0" | " 0 (kJ/mol)" |
Van der Waals over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "LJ-SR:Protein-non-Protein" | "-2172.28" | "15" | "136.956" | "-103.12 (kJ/mol)" |
| "LJ-14:Protein-non-Protein" | " 0" | " 0" | " 0" | " 0 (kJ/mol)" |
Questions
1. What is the average temperature and what is the heat capacity of the system?
The average temperature of our system is 297.886 K and the heat capacity ranges from 303 to 292. (values taken from figure 3).
2. What are the terms plotted in the files energy.xvg and box.xvg
In energy.xvg we plot the energy values of kinetic energy, potential energy and total energy over the time of our simulation.
In box.xvg we plot the size of the box around our protein which is given in nm.
3. Estimate the plateau values for the pressure, the volume and the density.
We consider the plateau value as two values, the upper and lower plateau. These plateaus represent the maximum and minimum values of our given plots.
Pressure:
- upper plateau:450 bar
- lower plateau: -450 bar
Volume:
- upper plateau: 357.9 nm^3
- lower plateau: 355.8 nm^3
Density:
- upper plateau: 1026 kg/m^3
- lower plateau: 1017 kg/m^3
4. What are the terms plotted in the files coulomb-inter.xvg and vanderwaals-inter.xvg
The coloumb and van der waals energys of our WT over time.
MINIMUM DISTANCES BETWEEN PERIODIC IMAGES
We ran gromacs with the following command:
//when asked for group selection we selected group 1
g_mindist -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -od /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/minimal-periodic-distance.xvg -pi
And produced the plot seen in figure 11.
In a next step we produced a plot which only uses the C-alpha atoms to calculate the minimum distance between periodic images. For this we used the same command as before. Although, we selected group 3 this time. The result can be seen in figure 12.
Questions
What was the minimal distance between periodic images and at what time did that occur?
The shortest periodic distance is 1.73442 (nm) at time 2720 (ps), between atoms 563 and 5314.
What happens if the minimal distance becomes shorter than the cut-off distance used for electrostatic interactions? Is it the case in your simulations?
If the distance would become shorter than the cut-off distance used for electrostatic interactions our energy would dramatically increase. This did not happen for our simulation so we can assume that our measured value of 1.73 nm is still higher than the cutoff.
Run now g_mindist on the C-alpha group, does it change the results? What does is mean for your system?
With C-alpha group we got a shortest periodic distance of 2.4249 (nm) at time 6805 (ps), between atoms 589 and 5297. This is an increase of the distance since we only consider C-alpha atoms and no side chains as in our previous calculation.
ROOT MEAN SQUARE FLUCTUATIONS
In this part of the analysis we are going to have a look at the root mean square fluctuations. By analyzing this value for our structure we might be able to figure out which parts of our protein are more flexible than others.
To do so we executed the following command:
g_rmsf -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsf-per-residue.xvg -ox /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/average.pdb -oq /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/bfactors.pdb -res
Which gives us three result files:
- rmsf-per-residue.xvg : this file contains a plot over the whole structure length of the RMSF values
- average.pdb : is the average conformation of the structure
- bfactors.pdb: assigned b factor values to the residues which gives us information about the flexibility
RMSF of Protein
We can see a remarkable peak at the beginning of the protein. Which means that this part is more flexible.
RMSF of C-alpha
The 3D view figures in pymol could not be created. There was no structure present if C-alpha is used.
In contrast to the whole protein RMSF calculation this plot seems to be more noise free. Here we can see a strong contrast of the beginning of the protein to the rest.
Questions
Indicate the start and end residue for the most flexible regions and the maximum amplitudes.
The most flexible region in our structure is from position 131 to 152 which is a loop connecting two alpha-helices. This can be observed in the plot in figure 13 as well as in the 3D view of our protein in figure 14. In general we can say that most of the parts are rather rigid, especially the residues which are located within the core. We observe slightly more flexibility in some alpha-helices which are located at the surface of the protein. Such as the residues located at position 197, 208, 215 and 216. There are also some beta-sheets which contain slightly flexible residues such as residues at position 413 and 420.
CONVERGENCE OF RMSD
It is adviced in the tutorial to remove the jumps of our protein and bring it back to the middle. This is done with the following command:
trjconv -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -o 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -pbc nojump
Then we calculated the RMSD for the whole protein and a second time only for the backbone with the following command:
//whole protein: select 1 and 1 again
g_rms -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-all-atom-vs-start.xvg
//backbone only: select 4 and 4 again
g_rms -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-backbone-vs-start.xvg
After that we calculated the RMSD for the average protein structure with the following commands, once for the whole protein and once for the backbone only:
trjconv -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/protein.xtc
g_rms -f /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/protein.xtc -s /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/average.pdb -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-all-atom-vs-average.xvg
g_rms -f /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/protein.xtc -s /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/average.pdb -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-backbone-vs-average.xvg
We received then the following results:
Questions
If observed, at what time and value does the RMSD reach a plateau?
We observed in the figures (16-17, against start structure) that the plateau is reached after 5000ps with the following approximated values:
- All atom vs start: 0.225
- Backbone vs start: 0.175
For the average structures we observed that the plateau is reached earlier after 300ps with the following approximated values:
- All atom vs average: 0.16
- Backbone vs average: 0.125
Briefly discuss two differences between the graphs against the starting structure and against the average structure. Which is a better measure for convergence?
As we can see the plateau is reached earlier in the average structure than in the start structure. The reason for this might be that the average structure is closer to the equilibrium than the start structure. Hence, also the RMSD values are lower here.
Since the average structures converges earlier than the starting structure we think that this plots are the better ones to judge whether convergence has been reached or not.
CONVERGENCE OF RADIUS OF GYRATION
To calculate the radius of gyration we executed the following command:
g_gyrate -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/radius-of-gyration.xvg
And received the following plot :
Questions
At what time and value does the radius of gyration converge?
The radius of gyration fluctuates between 1.90 to 1.95 nm. The value for RGz is fluctuating between 1.55 to 1.70, RGx is fluctuating between 1.45 to 1.70 and RGy is fluctuating between 1.45 to 1.55.
STRUCTURAL ANALYSIS: PROPERTIES DERIVED FROM CONFIGURATIONS
SOLVENT ACCESSIBLE SURFACE AREA
In this part of our analysis we are checking the solvent accessible area of our protein over time. To calculate these values we executed the following command:
// select 1 and 1 again when asked for group
g_sas -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/solvent-accessible-surface.xvg -oa /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/atomic-sas.xvg -or /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/residue-sas.xvg
We received the following 3 output plots:
The fluctuation as seen in figure 21 for hydrophobic areas is around 95nm^2 and very constant over time. The same applies for the hydrophilic areas which is around 80nm^2 and therefore is slightly lower than the hydrophobic areas. However the value over time stays very constant as well here.
If we have a look on the solvent accessibly per residue as seen in figure 23 we can observe that the values here are strongly fluctuating all over the whole length of the protein. However, we might be able to observe a trend. It seems like that the residues from 250 to 300 are less accessible than the parts at the N and C terminal ends.
HYDROGEN BONDS
In this part of our analysis we are looking at inter H-bonds within our protein and at H-bonds from our protein to the surrounding solvent. To do so we executed the following command twice:
// first time with 1 and 1 again to calculate inter H-bonds
// second time with 1 and 12 to calculate H-bonds from the protein to the surrounding solvent
g_hbond -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -num /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/hydrogen-bonds-protein-water.xvg
We received the following results seen in the figures below:
Questions
Discuss the relation between the number of hydrogen bonds for both cases and the fluctuations in each.
In figure 24 you can see the fluctuations over time of intra hydrogen bonds. The number of bonds for this case is around 1050 fluctuating over time with 50-100. Thus we can say that the number of intra hydrogen bonds stays quite stable during our simulation. However, the number of pairs within 0.35nm is significantly smaller, to be more precise the number is around 250.
The same applies for our protein to solvent hydrogen bonds as well. Here, as seen in figure 25 we only have a number of around 750 hydrogen bonds with a fluctuation of 50 to 100 over time which is similar stable as for the intra hydrogen bonds. However, the number of hydrogen bonds within 0.35nm is closer to the overall hydrogen bond count which is around 600.
RAMACHANDRAN (PHI/PSI) PLOTS
In this part of the analysis we have a look at the phi/psi angles in our protein. To do the calculations we executed the following command:
g_rama -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/ramachandran.xvg
We received the following plot:
 Figure 27: General ramachandran plot. redistributed from http://en.wikipedia.org/wiki/File:Ramachandran_plot_general_100K.jpg |
The ramachandran plot received from our WT looks somehow similar. Although, there are distinguishable differences as well. The areas around 100/-100 and -100/-100 for beta sheets and alpha helices are very well conserved if compared to the general ramachandran plot as seen in figure 26. However, there are some regions over represented in our WT. For example the -180/180 and the 180/180 region.
ANALYSIS OF DYNAMICS AND TIME-AVERAGED PROPERTIES
ROOT MEAN SQUARE DEVIATIONS AGAIN
In this part of the analysis we calculate the RMSD of our structure versus our structure over time. To do so we executed the following two commands:
//RMSD calculation
g_rms -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -f2 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -m rmsd-matrix.xpm -dt 10
//coloring of plot
xpm2ps -f rmsd-matrix.xpm -o rmsd-matrix.eps -rainbow blue
Finally we received the following plot:
Questions
What is interesting by choosing the group "Mainchain+Cb" for this analysis? Think about the different proteins used for this practical.
By using Mainchain+Cb we are considering the position of the C-beta atom as well for our RMSD calculation. The C-beta gives us information about the pointing position of our side chains which is a important feature when comparing two structures.
What can you conclude from this analysis? Could you expect such a result, justify?
From the plot seen in figure 27 we can see that the conformation at the end of the simulation is strongly different from that at the end . This can be somehow justified in a sense that the our protein gets more and more into equilibrium during simulation and therefore differs more and more from the beginning state.
Cluster Analysis
//when asked for input select 6 and 6 again
g_cluster -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -dm /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-matrix.xpm -dist /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/rmsd-distribution.xvg -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/clusters.xpm -sz /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/cluster-sizes.xvg -tr /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/cluster-transitions.xpm -ntr /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/cluster-transitions.xvg -clid /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/cluster-id-over-time.xvg -cl /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/clusters.pdb -cutoff 0.1 -method gromos -dt 10
We performed two cluster analysis calculations, one with a cutoff of 0.1 and another one with a cutoff of 0.13. This was necessary in order to receive a smaller amount of clusters with a bigger size. For our first cutoff we got 143 clusters which are too many. Therefore we increased the cutoff to 0.13 which resulted in 22 clusters.
0.1 Cutoff
0.13 Cutoff
Questions
How many clusters were found and what were the sizes of the largest two?
For our run with a cutoff of 0.13 we received 22 clusters with a size of 175 and 170 for the two biggest clusters as seen in figure 33. When looking at the cluster assignment for the different ids over time we notice that for a cutoff of 0.13 that most ids belong to the lower clusters and that this is constant during the whole simulation time. However, at time point 8000ps we observe the formation of cluster one at which most ids stay.
DISTANCE RMSD
For this part of our analysis we have a look at the distance RMSD. The disadvantage of the normal RMSD calculation is that the value for the RMSD depends on the fitting of the two structures to compare. However, with distance RMSD inter atomic distances are compared, thus fitting is not required. To calculate the distance RMSD we executed the following command:
//select 1 and 1 again when asked for input
g_rmsdist -s 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md.tpr -f 1J8U_nosol_after_SCWRL_no_h_merged_crystal_water_md_nojump.xtc -o /home/student/Dropbox/Studium/3_semester/master_praktikum/task10/distance-rmsd.xvg
We received the following result:
Questions
At what time and value does the dRMSD converge and how does this graph compare to the standard RMSD?
As seen in figure 36 the RMSD increases more and more over time. It first starts with 0.1 and then increases to 0.2 to towards the end and finally reaches an RMSD of around 0.175 at the end. When compared to the RMSD calculation in figure 16 we can observe that the trend of the two plots is pretty much the same.
P281L
A BRIEF CHECK OF RESULTS
In order to verify that our simulation ran successfully we used the command line tool gmxcheck. we executed it as follows for our .xtc file:
gmxcheck -f P281L_md.xtc
How many frames are in the trajectory file and what is the time resolution?
We observed 2001 frames with a time resolution of 5ps.
How long did the simulation run in real time (hours), what was the simulation speed (ns/day) and how many years would the simulation take to reach a second?
The simulation ran 3h14 and had a simulation speed of 73.133 ns/day. To calculate 1 second we would need 0.328*10^9/(365*24) = 37442.92 years
Which contribution to the potential energy accounts for most of the calculations?
- potential energy: -4.57346e+05 kJ/mol
- greatest contribution by Coulomb: -4.45954e+05 kJ/mol
VISUALIZATION OF RESULTS
We extracted 1000 frames from the trajectory (-dt 10), leaving out the water (selected Protein when asked for a selection). Moreover, we will remove the jumps over the boundaries and make a continuous trajectory (-pbc nojump):
trjconv -s P281L_md.tpr -f P281L_md.xtc -o protein.pdb -pbc nojump -dt 10
After that we opened the generated protein.pdb file with pymol.
QUALITY ASSURANCE
CONVERGENCE OF ENERGY TERMS
In this part of quality assurance we analyze different metrics of our MD simulation by creating plots from our *.edr file. We created plots for for pressure, temperature, potential and total energy of our MD simulation.
Temperature Over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Temperature" | 297.887 | 0.0054 | 1.58026 | 0.0204823 |
In figure 37 we can see that the temperature stays quite the same over the whole simulation. The average temperature is the same as in the WT simulation, the RMSD is slightly higher. That means we have more or greater outliers. Regarding the plot, we suggest that there are more outliers. There is especially one at about 8500 ps with a very high temperature. Such a high temperature could not be seen in the WT simulation. But there are only few differences, therefore we suggest, that the differences are not due to our mutation but that the differences are caused by the non-deterministic simulation process. The temperature has reached some kind of convergence. Therefore the simulation was probably successful.
Pressure over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Pressure" | 1.01427 | 0.011 | 133.436 | -0.0559964 |
Like in the analysis of the pressure, there seems to be no dramatic change compared to the WT simulation. It seems, that the pressure also converges in the simulation of the mutation. Therefore the simulation was probably successful.
Energies over Time
Total Energy
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Total Energy" | -375514 | 53 | 783.088 | -307.507 |
Potential Energy
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Total Energy" | -457346 | 54 | 638.456 | -313.132 |
In the potential and the total energy statistic for the mutation, we can observe a decrease in the energies for the first 4000 ps. Afterwards the energy converges. Therefore we assume that the simulation of the mutation was successful.
MINIMUM DISTANCES BETWEEN PERIODIC IMAGES
We check the shortest periodic distances, because we want to avoid interactions between a atom to itself in two periodic images. Such an unphysical interaction would dramatically influence the simulation. The result would be nonsense.
The shortest periodic distance in the whole protein is 1.9083 (nm) at time 55 (ps), between atoms 1198 and 5323. The shortest periodic distance between two C-alpha is 2.75268 nm at time 2320 ps, between atoms 2715 and 5306.
Therefore we suggest, that no such unphysical interaction occurred in the simulation.
ROOT MEAN SQUARE FLUCTUATIONS
In this part of the analysis we are going to have a look at the root mean square fluctuations. By analyzing this value for our structure we might be able to figure out which parts of our protein are more flexible than others.
Compared to the WT simulation the peak at about residue 45 in the RMSF per residue plot decreased from 0.45 to 0.275 RMSF. This might happen due to the non-deterministic simulation process, but the rest of the plot seems to be untouched. Therefore we assume it could be an effect of the mutation. Due to the similarity to the WT simulation and our decision about its quality, we can call the mutation simulation also successful.
CONVERGENCE OF RADIUS OF GYRATION
The plots for the gyration of the WT and of the mutation are quite different. But this might be due to the "non-deterministic" simulation process. But this is not essential for the quality assessment. The overall gyration radius is quite stable at 1.94 nm. The gyration radius of the three axis are converging. RgX and RgY are quite overlapping. Wheras RgZ converges with the RgX and RgY at about 1.4 nm. Therefore we can assume, that the simulation was successful.
STRUCTURAL ANALYSIS: PROPERTIES DERIVED FROM CONFIGURATIONS
SOLVENT ACCESSIBLE SURFACE AREA
There seems to be no difference to the WT simulation.
HYDROGEN BONDS
In this part of our analysis we are looking at inter H-bonds within our protein and at H-bonds from our protein to the surrounding solvent.
The hydrogen bonds within the protein seems to be untouched by the mutation. Whereas the hydrogen bonds of the protein to the water show a significant difference. In the WT there is a increase in hydrogen bonds from 5500 ps to 8000 ps. This "wave" is missing in the plot of the mutation's simulation. Perhaps this is just a result of the non-deterministic simulation process. Therefore it is probably caused by the mutation.
RAMACHANDRAN (PHI/PSI) PLOTS
In the mutant P281L there is a great change in the ramachandran plot compared to the md simulation of the native protein. In the native structure there are residues, which could express a positive Phi-angle and a Psi-angle greater than one hundred. It seems that some residues have lost their capability to express this angle combination.
Comparing the native conformation and the mutated conformation of residue 281 a greater divergence in the Phi-angle is observable.
It seems that the mutated structure has lost some degrees of freedom of some residues compared to the native structure. If this change is located at the loops of the entry site, this might explain the differences of the hydrogen bonds to the water.
ANALYSIS OF DYNAMICS AND TIME-AVERAGED PROPERTIES
RMSD matrix
We suggested in the structure based prediction of P281L, that the mutation can cause a dramatic change in the conformation of protein. The proline is located at the end of a helix in the catalytic site of the protein. In the mutated structure the helix might be greater and this extension might cause dramatic changes in the catalytic site.
The two RMSD matrices of the native structure and the P281L structure are quite similar. But the degree of difference in RMSD between two close conformations of the structure are much lower in the native structure. The greater difference in the mutant might be caused by the suggested conformational change.
Cluster analysis
Compared to the native simulation, in the mutant were much more clusters found (native 50; mutant 250). This probably means, that some long-term conformational changes are caused by the mutation in the md simulation. Many of the clusters of the mutant are quite empty (250 with just one member; in the native 50 with just one member). This observation enforces our theory of the conformational change caused by the mutation.
Distance RMSD
R408W
A BRIEF CHECK OF RESULTS
In order to verify that our simulation ran successfully we used the command line tool gmxcheck. we executed it as follows for our .xtc file:
gmxcheck -f R408W_md.xtc
How many frames are in the trajectory file and what is the time resolution?
We observed 2001 frames with a time resolution of 5ps.
How long did the simulation run in real time (hours), what was the simulation speed (ns/day) and how many years would the simulation take to reach a second?
The simulation ran 4h07 and had a simulation speed of 76.846 ns/day. To calculate 1 second we would need 0.312*10^9/(365*24)= 35616.43 years
Which contribution to the potential energy accounts for most of the calculations?
- potential energy: -4.57166e+05 kJ/mol
- greatest contribution by Coulomb: -4.46176e+05 kJ/mol
VISUALIZATION OF RESULTS
We extracted 1000 frames from the trajectory (-dt 10), leaving out the water (selected Protein when asked for a selection). Moreover, we will remove the jumps over the boundaries and make a continuous trajectory (-pbc nojump):
trjconv -s R408W_md.tpr -f R408W_md.xtc -o protein.pdb -pbc nojump -dt 10
After that we opened the generated protein.pdb file with pymol.
QUALITY ASSURANCE
CONVERGENCE OF ENERGY TERMS
In this part of quality assurance we analyze different metrics of our MD simulation by creating plots from our *.edr file. We created plots for for pressure, temperature, potential and total energy of our MD simulation.
Temperature Over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| Temperature | 297.883 | 0.008 | 1.57981 | -0.00616634 |
In figure 59 we can see that the temperature stays quite the same over the whole simulation. The average temperature is the same as in the WT simulation, the RMSD is slightly higher. There are only few differences, therefore we suggest, that the differences are not due to our mutation but that the differences are caused by the non-deterministic simulation process. The temperature has reached some kind of convergence. Therefore the simulation was probably successful.
Pressure over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Pressure" | 1.0242 | 0.03 | 133.452 | -0.0978398 |
Like in the analysis of the pressure, there seems to be no dramatic change compared to the WT simulation. It seems, that the pressure also converges in the simulation of the mutation. Therefore the simulation was probably successful.
Total Energy over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Total Energy" | -375304 | 46 | 779.24 | -291.686 |
Potential Energy over Time
| "Energy" | "Average" | "Err.Est." | "RMSD" | "Tot-Drift" |
| "Potential Energy" | -457166 | 46 | 634.117 | -289.993 |
In the potential energy statistic for the mutation, we can observe a decrease in the energies for the first 3000 ps. Afterwards the energy converges. The and the total energy statistic seems to be quite "constant" over the whole simulation. Therefore we assume that the simulation of the mutation was successful.
MINIMUM DISTANCES BETWEEN PERIODIC IMAGES
We check the shortest periodic distances, because we want to avoid interactions between a atom to itself in two periodic images. Such an unphysical interaction would dramatically influence the simulation. The result would be nonsense.
The shortest periodic distance in the whole protein is 1.84197 (nm) at time 6060 (ps), between atoms 564 and 5318. The shortest periodic distance between two C-alpha is 2.50235 (nm) at time 5690 (ps), between atoms 569 and 5297.
Therefore we suggest, that no such unphysical interaction occurred in the simulation.
ROOT MEAN SQUARE FLUCTUATIONS
In this part of the analysis we are going to have a look at the root mean square fluctuations. By analyzing this value for our structure we might be able to figure out which parts of our protein are more flexible than others.
There are almost no differences between the WT simulation and the R408W simulation in the RMSF. Due to the similarity to the WT simulation and our decision about its quality, we can call the mutation simulation also successful.
CONVERGENCE OF RADIUS OF GYRATION
The plots for the gyration of the WT and of the mutation R408W are quite different. But this might be due to the "non-deterministic" simulation process. But this is not essential for the quality assessment. The overall gyration radius is quite stable at 1.9 nm. RgX and RgY seem to converge at 1.4 nm. RgZ seems to converge at 1.7 nm. Therefore we can assume, that the simulation was successful.
STRUCTURAL ANALYSIS: PROPERTIES DERIVED FROM CONFIGURATIONS
SOLVENT ACCESSIBLE SURFACE AREA
There seems to be no difference to the WT simulation.
HYDROGEN BONDS
In this part of our analysis we are looking at inter H-bonds within our protein and at H-bonds from our protein to the surrounding solvent. To do so we executed the following command twice:
There seems to be no difference compared to the WT simulation.
RAMACHANDRAN (PHI/PSI) PLOTS
In the overall ramachandran plot the region around the psi-angle 100 and the phi-angle 200 and the region around the psi-angle 100 and the phi-angle -200 seems to be less populated than in the WT. The residue 408 shows in the WT and in the mutated simulation some outliers, but the main population site is quite the same.