Difference between revisions of "MD Mutation485"
(→solvent accesible surface area) |
(→solvent accessible surface area) |
||
| (65 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
=== check the trajectory === |
=== check the trajectory === |
||
| − | We checked the trajectory |
+ | We checked the trajectory and got following results: |
| − | |||
| − | gmxcheck -f mut436_md.xtc |
||
| − | |||
| − | With the command we got following results: |
||
Reading frame 0 time 0.000 |
Reading frame 0 time 0.000 |
||
| Line 31: | Line 27: | ||
| - |
| - |
||
|- |
|- |
||
| + | |Coordinates |
||
| − | |Coords |
||
|2001 |
|2001 |
||
|5 |
|5 |
||
| Line 49: | Line 45: | ||
|} |
|} |
||
| − | The simulation finished on node 0 Thu |
+ | The simulation finished on node 0 Thu September 15 19:12:47 2011. |
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 66: | Line 62: | ||
|} |
|} |
||
| − | The complete simulation needs 6 hours and 12 minutes |
+ | The complete simulation needs 6 hours and 12 minutes runtime. |
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 83: | Line 79: | ||
|} |
|} |
||
| − | As you can see in the table above, it takes about 2/3 hour to simulate 1 ns of the system. So therefore, it would be possible to simulate about |
+ | As you can see in the table above, it takes about 2/3 hour to simulate 1 nano second (ns) of the system. So therefore, it would be possible to simulate about 37 ns in one complete day calculation time. |
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | === Visualize in pymol === |
||
| + | <br><br> |
||
| + | === Visualize in PyMol === |
||
| − | First of all, we visualized the simulation with with ngmx, because it draws bonds based on the topology file. ngmx gave the user the possibility to choose different parameters. Therefore, we decided to visualize the system with following parameters: |
||
| + | |||
| + | First of all, we visualized the simulation with ngmx, because it draws bonds based on the topology file. ngmx gave the user the possibility to choose different parameters. Therefore, we decided to visualize the system with following parameters: |
||
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 112: | Line 111: | ||
Figure 1 shows the visualization with ngmx: |
Figure 1 shows the visualization with ngmx: |
||
| − | [[Image:mut485_ngmx.png|thumb|center|Figure 1: |
+ | [[Image:mut485_ngmx.png|thumb|center|Figure 1: Visualization of the MD simulation for mutation 436 with ngmx]] |
| + | Furthermore, we also want to visualize the structure with PyMol, which can be seen on Figure 2. |
||
| − | === create a movie === |
||
| + | [[Image:mut485.png|thumb|center|Figure 2: Visualization of the MD simulation for mutation 485 with PyMol]] |
||
| − | Next, we want to visualize the protein with pymol. Therefore, we extracted 1000 frames from the trajectory, leaving out the water and jump over the boundaries to make continuse trajectories. Therefore, we used following command: |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | trjconv -s fole.tpr -f file.xtc -o output_file.pdb -pbc nojump -dt 10 |
||
| + | <br><br> |
||
| + | |||
| + | === Create a movie === |
||
| + | |||
| + | Next, we want to visualize the protein with PyMol. Therefore, we extracted 1000 frames from the |
||
| + | trajectory, leaving out the water and jump over the boundaries to make continuous trajectories. |
||
| + | |||
| + | The program asks for a group as output. We only want to see the protein, therefore we decided to choose group 1. |
||
| + | |||
| + | Here you can see the movie in stick line and cartoon modus. |
||
| + | |||
| + | {| |
||
| + | |[[Image:mut485_animation.gif|thumb|center|Figure 3: Movie of the motion of mutation 485 in stick view.]] |
||
| + | |[[Image:mut485_antimation_1.gif|thumb|center|Figure 4: Movie of the motion of mutation 485 in cartoon view]] |
||
| + | |} |
||
| − | + | On Figure 3 and Figure 4, we can see that motion of the protein over time, which was created by the MD simulation. |
|
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | Todo: film und filtered |
||
| + | <br><br> |
||
=== energy calculations for pressure, temperature, potential and total energy === |
=== energy calculations for pressure, temperature, potential and total energy === |
||
| Line 153: | Line 168: | ||
[[Image:mut485_md_pressure.png|thumb|center|Figure 5: Plot of the pressure distribution of the MD system.]] |
[[Image:mut485_md_pressure.png|thumb|center|Figure 5: Plot of the pressure distribution of the MD system.]] |
||
| − | As you can see in Figure 5, the pressure fluctuates in the system around 0 and does mostly not exceed 100. Contrary,there are some |
+ | As you can see in Figure 5, the pressure fluctuates in the system around 0 and the amplitude does mostly not exceed 100. Contrary,there are some outliers which reach values of almost 250 and -250 bar. In this cases we are not sure, if a protein works under such a high pressure. |
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
==== Temperature ==== |
==== Temperature ==== |
||
| Line 171: | Line 189: | ||
|- |
|- |
||
|Minimum (in K) |
|Minimum (in K) |
||
| − | |294. |
+ | |294.99 |
|- |
|- |
||
|Maximum (in K) |
|Maximum (in K) |
||
| − | |301. |
+ | |301.08 |
|} |
|} |
||
The plot with the temperature distribution of the system can be seen here: |
The plot with the temperature distribution of the system can be seen here: |
||
| − | [[Image:mut485_md_temp.png|thumb|center|Figure |
+ | [[Image:mut485_md_temp.png|thumb|center|Figure 6: Plot of the temperature distribution of the MD system.]] |
| + | |||
| + | Figure 6 displays the distribution of the temperature in the current MD system. In this case the temperature fluctuates around 298K. The maximal occurring amplitude between the average and the outliers temperature is only about 4 K which is not much. But we have to keep in mind, that only some degree difference can affect huge functional loss of a protein. 298 K corresponds to 25°C, which is relatively low for human protein activity, because the highest activity is normally reached at body temperature which is about 36°C. |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | Figure 2 displays the distribution of the temperature in the current MD system. In this case the temperature fluctuates around 298K. The maximal occuring amplitude between the average and the outlier temperature is only about 3 K which is not much. But we have to keep in mind, that only some degree difference can affect huge functional loss of a protein. 298 K corresponds to 25°C, which is relatively low for human protein activity, because the highest activity is normally reached at body temperature which is about 37°C. |
||
| + | <br><br> |
||
==== Potential ==== |
==== Potential ==== |
||
| Line 199: | Line 220: | ||
|- |
|- |
||
|Minimum (in kJ/mol) |
|Minimum (in kJ/mol) |
||
| + | | -1.28513e+06 |
||
| − | | |
||
|- |
|- |
||
|Maximum (in kJ/mol) |
|Maximum (in kJ/mol) |
||
| + | | -1.27769e+06 |
||
| − | | |
||
|- |
|- |
||
|} |
|} |
||
| Line 208: | Line 229: | ||
The plot with the potential energy distribution of the system can be seen here: |
The plot with the potential energy distribution of the system can be seen here: |
||
| − | [[Image:mut485_md_potential.png|thumb|center|Figure |
+ | [[Image:mut485_md_potential.png|thumb|center|Figure 7: Plot of the potential energy distribution of the MD system.]] |
| − | Figure |
+ | Figure 7 displays the potential energy of the system which is between -1.28513e+06 and -1.27769e+06. This is a relatively low energy. Therefore, this probably means that the protein is stable. Furthermore, we can suggest, that the protein with such a low energy is stable and able to function. Therefore, our simulation is probably true. Otherwise, if the energy of the simulated system would be too high, we can not trust the results, because the protein is too instable to work. |
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
==== Total energy ==== |
==== Total energy ==== |
||
| Line 237: | Line 261: | ||
The plot with the total energy distribution of the system can be seen here: |
The plot with the total energy distribution of the system can be seen here: |
||
| − | [[Image:mut495_md_energy.png|thumb|center|Figure |
+ | [[Image:mut495_md_energy.png|thumb|center|Figure 8: Plot of the total energy distribution of the MD system.]] |
| − | Looking at Figure |
+ | Looking at Figure 8, we can see that the total energy deviates a little from the potential energy which is minimal lower. In this case, the total energy is between -1.055e+06 and -1.045e+06. These values lie already in a range, where we can suggest that the protein energy is sufficient low so that this one can work. |
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
=== minimum distance between periodic boundary cells === |
=== minimum distance between periodic boundary cells === |
||
| Line 246: | Line 273: | ||
Here you can see the result of this analysis: |
Here you can see the result of this analysis: |
||
| + | |||
| − | {| |
||
| − | + | [[Image:mut485_md_mindist2.png|thumb|center|Figure 9: Plot of the minimum distance between periodic boundary cells.]] |
|
| + | |||
| − | |[[Image:mut485_md_mindist2.png|thumb|center|Figure 7: Plot of the minimum distance between periodic boundary cells.]] |
||
| + | |||
| + | {| border="1" style="text-align:center; border-spacing:0;" |
||
| + | |Average (in nm) |
||
| + | |3.215 |
||
| + | |- |
||
| + | |Minimum |
||
| + | |1.772 |
||
| + | |- |
||
| + | |Maximum |
||
| + | |4.217 |
||
| + | |- |
||
|} |
|} |
||
| + | Figure 9 displays the minimum distance between periodic boundary cells at different time steps. It can be seen that there are huge differences between the distances at different times. The highest distance is 4.217 nm, whereas the smallest distance is only 1.772 nm. This means that there are some states during the simulation in which the interacting atoms are close together. Contrary, there are some states in which the atoms who interact are far away. Because of the huge bandwidth of minimum distance we can conclude, that the protein is flexible. |
||
| − | **************************** Hier noch ändern: *************************** |
||
| + | |||
| − | Figure 6 and 7 display.... |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | , there is a huge difference between the different time steps and distances. The highest distance is up to 4 nm, whereas the smallest distance is only about 1nm. Therefore, we can see that the protein is very flexible over the time. |
||
| + | <br><br> |
||
=== RMSF for protein and C-alpha === |
=== RMSF for protein and C-alpha === |
||
| Line 261: | Line 300: | ||
First of all, we calculate the RMSF for the whole protein. |
First of all, we calculate the RMSF for the whole protein. |
||
| − | The analysis produce two different pdb files, one file with the average structure of the protein and one file with high B-Factor values, which means that the high |
+ | The analysis produce two different pdb files, one file with the average structure of the protein and one file with high B-Factor values, which means that the high flexible regions of the protein are not in accordance with the original PDB file. |
| − | To compare the structure we align them with |
+ | To compare the structure we align them with PyMol to the original structure. |
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 272: | Line 311: | ||
|colspan="3" | Perspective one |
|colspan="3" | Perspective one |
||
|- |
|- |
||
| − | | [[Image:ali_average_original.png|thumb|Figure |
+ | | [[Image:ali_average_original.png|thumb|Figure 10: Alignment of the original structure (green) and the calculated average structure (turquoise)]] |
| − | | [[Image:ali_bfactor_original.png|thumb|Figure |
+ | | [[Image:ali_bfactor_original.png|thumb|Figure 11: Alignment of the original structure (green) and the calculated structure with high B-Factor values (turquoise)]] |
| − | | [[Image:ali_bfactor_average.png|thumb|Figure |
+ | | [[Image:ali_bfactor_average.png|thumb|Figure 12: Alignment of the structure with high B-Factor values (red) and the calculated average structure (blue)]] |
|- |
|- |
||
|colspan="3" | Perspective two |
|colspan="3" | Perspective two |
||
|- |
|- |
||
| − | | [[Image:ali_average_original_2.png|thumb|Figure |
+ | | [[Image:ali_average_original_2.png|thumb|Figure 13: Alignment of the original structure (green) and the calculated average structure (turquoise)]] |
| − | | [[Image:ali_bfactor_original_2.png|thumb|Figure |
+ | | [[Image:ali_bfactor_original_2.png|thumb|Figure 14: Alignment of the original structure (green) and the calculated structure with high B-Factor values (turquoise)]] |
| − | | [[Image:ali_bfactor_average_2.png|thumb|Figure |
+ | | [[Image:ali_bfactor_average_2.png|thumb|Figure 15: Alignment of the structure with high B-Factor values (red) and the calculated average structure (blue)]] |
|- |
|- |
||
|colspan="3" | RMSD |
|colspan="3" | RMSD |
||
| Line 290: | Line 329: | ||
|} |
|} |
||
| + | The RMSD as well as the structure alignment visualization indicates which structures are similar. In this case, the small RMSD at 0.349 as well as the structure alignment where the structures mostly agree indicates that the high B-factors agrees mostly with the original structure (Figure 11 and 14). The alignment of the original structure and the average structure delivers a higher disagreement (Figure 10 and Figure 13). There, the RMSD with 1.519 is much higher and the structure alignment is not extremely worse than the other one. |
||
| − | **************************** Hier noch ändern: *************************** |
||
| + | The regions with high B-Factors are usually very flexible. This means that the downloaded PDB structure is probably in another state, because of its flexible regions. |
||
| − | |||
| + | The low RMSD and the agreeing structure alignment of the high B-factor structure and the original one displays that the quality of |
||
| − | The structure with the high B-factors is the most similar structure (Figure 8 and Figure 11) compared with the original structure from PDB (Figure 7 and Figure 10). The average structure is not that similar (Figure 10 and Figure 12). But we know, that the regions with high B-Factors are very flexible, and therefore in the structure downloaded from the PDB, the protein is in another state, because of its flexible regions. Therefore, because of the low RMSD between the high B-factors structure and the original structure we can see, that the simulation predicts the structure quite good. |
||
| + | predicted structure is quite good. |
||
| − | |||
Furthermore, we got a plot of the RMSF values of the protein, which can be seen in Figure 13: |
Furthermore, we got a plot of the RMSF values of the protein, which can be seen in Figure 13: |
||
| − | [[Image:mut485_rmsf.png|thumb|center|Figure |
+ | [[Image:mut485_rmsf.png|thumb|center|Figure 16: Plot of the RMSF values over the whole protein.]] |
| + | There are two regions with very high RMSF values. The first one is at position 150 (Figure 17), and the second one is at position 350 (Figure 18). The structure alignment of the average structure and the original one shows that the most regions match with some exceptions. Therefore, we want to analysis, if these bad-matching regions are the regions with very high B-factor values. The following picture show the two regions around position 150 and 350 which have an arose RMSF. |
||
| − | **************************** Hier noch ändern: *************************** |
||
| − | There are two regions with very high B-factor values. One region at position 150 (Figure 14), and the other region at position 440 (Figure 15). If we compare the picture of the original and the average structure, we can see that most of the regions build a very good alignment, whereas some regions vary in their position. Therefore, we want to compare, if these regions are the regions with very high B-factor values. |
||
{| |
{| |
||
| − | | [[Image:mut485_peek1.png|thumb|Figure |
+ | | [[Image:mut485_peek1.png|thumb|Figure 17: Part of the alignment between the original structure and the average structure between residue 140 and 160.]] |
| − | | [[Image:mut485_peek2.png|thumb|Figure |
+ | | [[Image:mut485_peek2.png|thumb|Figure 18: Part of the alignment between the original structure and the average structure between residue 340 and 360.]] |
|} |
|} |
||
| − | Furthermore, we visualized the B-factors with the |
+ | Furthermore, we visualized the B-factors with the PyMol selection B-factor method at these two regions. We calculated the B-factors for the blue protein (Figure 19 and Figure 20). If you see red, this part of the protein is very flexible. The brighter the color, the higher is the flexibility of this residue. |
{| |
{| |
||
| − | | [[Image:mut485_bfact_zoom.png|thumb|Figure |
+ | | [[Image:mut485_bfact_zoom.png|thumb|Figure 19: Part of the alignment between the original structure and the average structure between residue 140 and 160. High B-Factor value -> bright color]] |
| − | | [[Image:mut485_bfact_zoom_2.png|thumb|Figure |
+ | | [[Image:mut485_bfact_zoom_2.png|thumb|Figure 20: Part of the alignment between the original structure and the average structure between residue 340 and 360. High B-Factor value -> bright color]] |
|} |
|} |
||
| + | The first picture displays the alignment around region 150. Here, we can see that the loop is colored in yellow and red. This bright colors show that the B-factor at this position is very high which indicates a higher flexibility. Contrary, the second picture for the region around residue 350 show only a small part in yellow and some parts in turquoise whereas the rest is colored in dark blue. Furthermore, the second peak is about 0.35 which does not stand for a high flexibility. All in all, this detailed views assume that there is only one region in the protein with a high flexibility. |
||
| − | **************************** Hier noch ändern: *************************** |
||
| − | In the second picture, you can see, that the color is dark blue. Therefore a peak lower than 0.3 do not mean that there is high flexibility. Therefore, our protein has only one very flexible region and this is around residue 140. |
||
| + | As you can see at the pictures above, especially at the first picture, which is the part with the highest peak in the plot, the structures have a very different position and the alignment in this part of the protein is very bad, although the rest of the alignment is quite good. That is also the reason for the relatively high RMSD which is caused by different position of the flexible parts of the protein. |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | As you can see in the pictures above, especially in the first picture, which is the part with the highest peak in the plot, the structures have a very different position and the alignment in this part of the protein is very bad, although the rest of the alignment is quite good. This also explains the relatively high RMSD values, because of the different positions of the flexible parts of the protein. |
||
| + | <br><br> |
||
==== C-alpha ==== |
==== C-alpha ==== |
||
| − | Now we repeat the analysis done for the protein for the C-alpha atoms of the protein. Therefore, we followed the same steps as in the section above. |
+ | Now we repeat the analysis, done for the protein, for the C-alpha atoms of the protein. Therefore, we followed the same steps as in the section above. |
| − | To compare the structure we align them with |
+ | To compare the structure we align them with PyMol with the original structure. |
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 333: | Line 372: | ||
|colspan="3" | Perspective one |
|colspan="3" | Perspective one |
||
|- |
|- |
||
| − | | [[Image:ali_average_ori_calpha.png|thumb|Figure |
+ | | [[Image:ali_average_ori_calpha.png|thumb|Figure 21: Alignment of the original structure (green) and the calculated average structure of the c-alpha atoms (turquoise)]] |
| − | | [[Image:ali_bfactor_ori_calpha.png|thumb|Figure |
+ | | [[Image:ali_bfactor_ori_calpha.png|thumb|Figure 22: Alignment of the original structure (green) and the calculated structure with high B-Factor values of the c-alpha atoms (turquoise)]] |
| − | | [[Image:ali_bfactor_average_calpha.png|thumb|Figure |
+ | | [[Image:ali_bfactor_average_calpha.png|thumb|Figure 23: Alignment of the structure with high B-Factor values of the c-alpha atoms (red) and the calculated average structure of the c-alpha atoms (blue)]] |
|- |
|- |
||
|colspan="3" | Perspective two |
|colspan="3" | Perspective two |
||
|- |
|- |
||
| − | | [[Image:average_ori_calpha_2.png|thumb|Figure |
+ | | [[Image:average_ori_calpha_2.png|thumb|Figure 24: Alignment of the original structure (green) and the calculated average structure of the c-alpha atoms (turquoise)]] |
| − | | [[Image:average_bfactor_ori_calpha_2.png|thumb|Figure |
+ | | [[Image:average_bfactor_ori_calpha_2.png|thumb|Figure 25: Alignment of the original structure (green) and the calculated structure with high B-Factor values of the c-alpha atoms (turquoise)]] |
| − | | [[Image:ali_bfactor_average_calpha_2.png|thumb|Figure |
+ | | [[Image:ali_bfactor_average_calpha_2.png|thumb|Figure 26: Alignment of the structure with high B-Factor values of the c-alpha atoms (red) and the calculated average structure of the c-alpha atoms (blue)]] |
|- |
|- |
||
|colspan="3" | RMSD |
|colspan="3" | RMSD |
||
| Line 351: | Line 390: | ||
|} |
|} |
||
| + | As in the section above, the RMSD between the structure with high B-factor values and the original structure is the most similar (Figure 22 and Figure 25). This was expected, because we used twice the same model, but in this case we neglected the residues of the atoms whereas the backbone of the protein remains the same. The other two models (Figure 21, Figure 23, Figure 24 and Figure 26) have nearly the same RMSD value and therefore there are equally. |
||
| − | |||
| − | ******************* Hier noch ändern ********************** |
||
| − | As in the section above, the RMSD between the structure with high B-factor values and the original structure is the most similar (Figure 19 and Figure 22). This was expected, because we used twice the same model, but in this case we neglecte the residues of the atoms. But the backbone of the protein remains the same. The other two models (Figure 18, Figure 20, Figure 21 and Figure 23) have nearly the same RMSD value and therefore there are equally. |
||
Furthermore, we got a plot of the RMSF values of the protein, which can be seen on Figure 24: |
Furthermore, we got a plot of the RMSF values of the protein, which can be seen on Figure 24: |
||
| − | [[Image:mut485_rmsf_calpha.png|thumb|center|Figure |
+ | [[Image:mut485_rmsf_calpha.png|thumb|center|Figure 27: Distribution of the b-factor values by only regarding the backbone of the protein.]] |
| + | In this case, there is only one high peak at position 150 (Figure 27). Having a closer look at the protein it can be seen that the position of the beta sheets differ extremely between the two models. |
||
| − | ******************* Hier noch ändern ********************** |
||
| − | + | The other peak at position 350 could not be found in the plot. Looking at the pictures above, we can see that the backbones of the two different models not differ extremely. This means that the position of the residues differ a lot, which is not important for us, because we do not regard side chains. |
|
=== Radius of gyration === |
=== Radius of gyration === |
||
| − | Next, we want to |
+ | Next, we want to analyze the Radius of gyration. Therefore we use g_gyrate and use only the protein for the calculation. |
| + | {| |
||
| − | [[Image:mut485_gyration_r.png|thumb|center|Figure 25: Plot with the distribution of the radius of gyration over time]] |
||
| + | |[[Image:mut485_gyration_r2.png|thumb|center|Figure 28: Plot with the distribution of the radius of gyration over time]] |
||
| + | |[[Image:mut485_gyration_r.png|thumb|center|Figure 29: Plot with the distribution of the radius of gyration over time for each axis]] |
||
| + | |} |
||
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 377: | Line 417: | ||
|Average |
|Average |
||
|2.416 |
|2.416 |
||
| − | |2. |
+ | |2.145 |
|1.630 |
|1.630 |
||
|2.094 |
|2.094 |
||
| Line 395: | Line 435: | ||
|} |
|} |
||
| + | Figure 28 shows the radius of gyration over the simulation time. The radius of gyration is the RMS distance from the outer parts of the protein to the protein center or gyration axis. The plot displays that the average radius is about 2.42 with some fluctuation. This indicates that the protein is flexible. Furthermore, the fluctuation is a periodic curve which shows the loss and the gain of space the protein needs. This suggest that the protein pulsates. |
||
| − | ******************* Hier noch ändern ********************** |
||
| + | |||
| − | Figure 25 shows the radius of gyration over the simulation time. The Radius of gyration is the RMS distance of its parts from its center or gyration axis. On the plot it could be seen, that the average radius is about 2.4, but there are big differences, which means, that the protein is flexible. The distance between the different parts of the protein and the center differs so the protein seems to pulsate, because there is a periodic curve which shows the loss and the gain of space the protein needs. |
||
| + | If we have a further look at the radius of the different axis (Figure 29), we can see, that the radius of the x coordinates is |
||
| + | the only consistent one at about 2nm during the simulation. The radius of the z axis shows deflection at the end of the simulation where it decreases. The y axis values, however, increase during the simulation and reaches the value of the decreased z-radius which is still smaller than the radius for the x-axis. This means that the motions in x and the motion in z at the beginning of the simulation has most influence on the whole gyration radius. |
||
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
| − | === solvent |
+ | === solvent accessible surface area === |
| − | Next, we |
+ | Next, we analyzed the solvent accessible surface area of the protein, which is the area of the protein which has contacts with the surrounding environment, mainly water. |
| − | First of all, we have a look at the solvent |
+ | First of all, we have a look at the solvent accessibility of each residue, which can be seen on Figure 27. Furthermore, we regard at the solvent accessibility area of each residue in the protein with standard deviation (Figure 28). |
{| |
{| |
||
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_residue2.png|thumb|center|Figure 30: Solvent accessibility area of each residue in the protein]] |
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_residue.png|thumb|center|Figure 31: Solvent accessibility area of each residue in the protein with standard deviation]] |
|} |
|} |
||
| − | The following table list the average, minimum and maximum values of the |
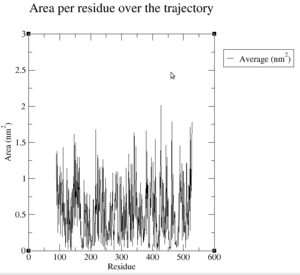
+ | The following table list the average, minimum and maximum values of the solvent accessibility for each residue in the protein. The residues at the beginning and at the end of the simulation which have a value of 0 are ignored. |
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| − | |Average (in nm |
+ | |Average (in nm²) |
|0.542 |
|0.542 |
||
|- |
|- |
||
| − | |Minimum (in nm |
+ | |Minimum (in nm²) |
|0.007 |
|0.007 |
||
|- |
|- |
||
| − | |Maximum (in nm |
+ | |Maximum (in nm²) |
|2.014 |
|2.014 |
||
|- |
|- |
||
|} |
|} |
||
| + | The average area per residue during the trajectory is between 0 and 2nm², as can be seen in Figure 30. Most of the residues have an area about 0.5nm². From this it follows that there are mainly sparse moving residues during the complete simulation with some exceptions where the residues are very flexible. In Figure 31, you can additionally see the standard deviation, which is very low and which indicates that there are no big outliers in there. This means that there is no big deviation from the average area so the residues behave in the same way during the trajectory. |
||
| − | Furthermore, it is also possible to look at the solvent accesibility of each atom of the complete protein, which can be seen on Figure 27. |
||
| + | |||
| + | Besides, we can analyze the position of the residues within the protein based on the solvent accessibility. First, we can see in Figure 30 that the first 100 and the last 100 residues have an average solvent accessibility of 0 which means that these residues are always completely in the interior of the protein. Most of the residues have a solvent accessibility about 0.5nm², and there are only some outliers with an accessibility of more than 1.5nm². This means that there are some residues which are almost always on the surface, a lot of residues which are partly or temporarily on the surface and a lot of residues which are never on the surface. |
||
| + | Looking at Figure 31, we can see that the standard deviation is relatively low. This means that there are no system states in which any residues with low or no solvent accessibility get complete accessible to the surface. If the standard deviation would be very high, it would indicate that there are some very unusual states in the simulation which is not the case in our simulation. |
||
| + | |||
| + | Furthermore, it is possible to look at the solvent accessibility of each atom of the complete protein, which can be seen in Figure 32 and Figure 33. |
||
{| |
{| |
||
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_atomic2.png|thumb|center|Figure 32: Solvent accessibility of each atom of the complete protein.]] |
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_atomic.png|thumb|center|Figure 33: Solvent accessibility of each atom of the complete protein with standard deviation.]] |
|} |
|} |
||
| Line 433: | Line 483: | ||
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| − | |Average (in nm |
+ | |Average (in nm²) |
|0.032 |
|0.032 |
||
|- |
|- |
||
| − | |Minimum (in nm |
+ | |Minimum (in nm²) |
|0 |
|0 |
||
|- |
|- |
||
| − | |Maximum (in nm |
+ | |Maximum (in nm²) |
|0.561 |
|0.561 |
||
|- |
|- |
||
|} |
|} |
||
| + | In Figure 32 the average area per atom is plotted, which deliver similar results to Figure 30. In general the atoms have not such a big area as the residues. This can be explained easily because the residue area is consisting of the single atom areas which belong to this residue. |
||
| − | Figure 29 shows how much of the area of the protein is accesibile to the surface during the complete simulation. As we saw before, by the gyration radius of the protein, the values differ during the simulation, which shows, that the protein is flexible. |
||
| + | There are a huge number of atoms which have an area of about 0nm². As before, the standard deviation is not that high (Figure 33). It is a little bit higher than than the one in Figure 28 which was expected, because of the smaller and more detailed scale of this Figure. In general Figure 32 and Figure 33 confirm the results of Figure 30 and Figure 31. |
||
| + | |||
| + | At the end of the plot, there are a lot of atoms which have a surface accessibility area of 0, which is consistent with the result for the residues. But at the beginning of the plot, there are no atoms which have no surface accessibility area. However, there are a lot of atoms with low or no accessibility area in the plot. |
||
| + | |||
| + | Figure 34 shows how much of the area of the protein is accessible to the surface during the complete simulation. As we saw before, by the gyration radius of the protein, the values differ during the simulation, which shows, that the protein is flexible. |
||
{| |
{| |
||
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_surf2.png|thumb|center|Figure 34: Area of the protein which is accessible to the surface during the simulation.]] |
| − | |[[Image: |
+ | |[[Image:mut485_md_solv_acc_surf.png|thumb|center|Figure 35: Area of the protein which is accessible to the surface during the simulation with standard deviation.]] |
|} |
|} |
||
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| − | |Average (in nm |
+ | |Average (in nm²) |
|135.452 |
|135.452 |
||
|- |
|- |
||
| − | |Minimum (in nm |
+ | |Minimum (in nm²) |
|129.167 |
|129.167 |
||
|- |
|- |
||
| − | |Maximum (in nm |
+ | |Maximum (in nm²) |
|142.977 |
|142.977 |
||
|- |
|- |
||
|} |
|} |
||
| + | Figure 34 and Figure 35 display the solvent accessibility surface of the whole protein during the simulation. The surface accessibility of the hydrophobic residues has an area of about 135nm², which is relatively consistent during the complete simulation. The second plot describes the solvent accessibility for different physicochemical properties. It shows that the accessibility rate of the hydrophobic amino acids is larger than of the hydrophilic amino acids which is unexpected. Normally, hydrophobic amino acids prefer a location in the core of the protein and not on the surface. |
||
| − | ******************* Hier noch ändern ********************** |
||
| + | |||
| − | So we can see in the pictures there are a lot of differences between the solvent accesibility of the protein's surface, which was expected. If we have a closer look at the plot about the atomic accesibility and the residue accesibility, we can see, that both pictures agree. During the simulation there is a big differences in the accessibility of the protein. There is a area between 131 and 146 nm/2S/N during the simulation, which is a big difference. Therefore, we can see that the protein has to be really flexible, otherwise, these different values could not be explained. |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
=== hydrogen-bonds === |
=== hydrogen-bonds === |
||
| − | + | As a next step we analysis the formed hydrogen bonds within the protein during the simulation. Here, we differ between hydrogen-bonds between the protein itself and bonds between the protein and the water. |
|
| − | + | The following plots display the number of hydrogen bonds within the protein over the simulation time. |
|
| − | On Figure 30 you can see the bonds between the protein. Here you can see that the number differs between 300 bonds and 355. Most of the time, the protein has between 320 and 330 hydrongen-bonds. |
||
{| |
{| |
||
| − | |[[Image: |
+ | |[[Image:mut485_md_number_intra2.png|thumb|center|Figure 36: Number of hydrogen-bonds in the protein over simulation time]] |
| − | |[[Image: |
+ | |[[Image:mut485_md_number_intra.png|thumb|center|Figure 37: Number of hydrogen-bonds and the possible hydrogen-bonds in the protein over simulation time]] |
|} |
|} |
||
| + | {| border="1" style="text-align:center; border-spacing:0;" |
||
| − | ******************* Hier noch ändern ********************** |
||
| + | | |
||
| − | If we have a look at the number of bonds between the protein and the water, which are visualized on Figure 31, we can see that there are a lot more bonds between protein and water than in between the protein. The number differs between 800 and 900 and there there are about 3 times more bonds between the protein and the water. Over the simulation time, the number of bonds between water and protein grows in average. But most of the time, the protein has between 840 and 860 bonds with the water. |
||
| + | |bonds in the protein |
||
| + | |possible bonds in the protein |
||
| + | |- |
||
| + | |Average |
||
| + | |323.337 |
||
| + | |1543.024 |
||
| + | |- |
||
| + | |Minimum |
||
| + | |300 |
||
| + | |1491 |
||
| + | |- |
||
| + | |Maximum |
||
| + | |354 |
||
| + | |1602 |
||
| + | |- |
||
| + | |} |
||
| + | |||
| + | In Figure 36 you can see the bonds within the protein. Here the number differs between 300 bonds and 355. Most of the time, the protein has between 320 and 330 hydrogen-bonds. Furthermore, it is possible to see in this plot, that the protein is flexible, because the number of bonds fluctuate extremely over the time. |
||
| + | |||
| + | Figure 37 displays the number of hydrogen bonds that occur during the simulation as well as all residue pairs with a distance smaller than 0.35nm which is the distance where a hydrogen bond is theoretically possible. This plot shows that there exist much more possible hydrogen bindings than occurred in real. Here the number of possible pairs is about 1500 whereas the number of formed hydrogen bond is only between 320 and 330 which is only about 20%. The small number of formed hydrogen bonds can indicate the high protein's flexibility. |
||
| + | |||
| + | The following plots display the number of hydrogen bonds between the protein and the surrounding water over the simulation time. |
||
{| |
{| |
||
| − | |[[Image: |
+ | |[[Image:mut485_md_number_water2.png|thumb|center|Figure 38: Number of hydrogen-bonds between the protein and the surrounding water.]] |
| − | |[[Image: |
+ | |[[Image:mut485_md_number_water.png|thumb|center|Figure 39: Number of hydrogen-bonds and the possible hydrogen-bonds between the protein and the surrounding water.]] |
|} |
|} |
||
| + | |||
| − | ******************* Hier noch ändern ********************** |
||
| + | {| border="1" style="text-align:center; border-spacing:0;" |
||
| − | This is no surprise, because every residue on the surface has contact with water, whereas in the protein there are a lot of amino acids which do not have contact partners, because the other amino acids are too far away. |
||
| + | | |
||
| + | |bonds between protein and water |
||
| + | |possible bonds between protein and water |
||
| + | |- |
||
| + | |Average |
||
| + | |847.965 |
||
| + | |999.310 |
||
| + | |- |
||
| + | |Minimum |
||
| + | |783 |
||
| + | |882 |
||
| + | |- |
||
| + | |Maximum |
||
| + | |912 |
||
| + | |1126 |
||
| + | |- |
||
| + | |} |
||
| + | |||
| + | Looking at the number of hydrogen bonds formed between the protein and the surrounding water, which is visualized in Figure 38, we can see that there exist much more bonds between protein and water than within the protein. The number differs between 800 and 900 which is about 3 times more than the number within the protein. Most of the time, the protein forms between 840 and 860 bonds with the surrounding water. |
||
| + | |||
| + | Figure 39 displays additional the number of residue pairs with a distance less than 0.35 nm which is the distance where a hydrogen bond is theoretically possible. The number of pairs within 0.35nm is about 1000. Compared to Figure 34 the distance of possible and real occurring hydrogen bonds is significantly lower. In this case, almost 80% of all possible hydrogen bonds are also real hydrogen bonds. Therefore, we can see that the binding between protein and water is really stable. |
||
| + | |||
| + | This is no surprise, because every residue on the surface has contact with water, whereas within the protein there are a lot of amino acids which have no contact partners, because of the big underlying distance to another amino acid. |
||
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
=== Ramachandran plot === |
=== Ramachandran plot === |
||
| − | Now, we want to have a closer look to the secondary structure of the protein during the simulation. Therefore, we used a Ramachandran plot to |
+ | Now, we want to have a closer look to the secondary structure of the protein during the simulation. Therefore, we used a Ramachandran plot to analyze the phi and psi torsion angles of the backbone to get a better understanding of the secondary structure during the simulation. |
| − | [[Image:mut485_ramachandran.png|thumb|center|Figure : Ramachandran Plot of the Mutation 485.]] |
+ | [[Image:mut485_ramachandran.png|thumb|center|Figure 40: Ramachandran Plot of the Mutation 485.]] |
| + | As we can see on Figure 40, there are a lot of beta sheets, alpha helices and right-handed alpha helices. The white regions are the regions where no secondary structure can be found. The white regions of our ramachandran plot agree with the white regions of a standard ramachandran plot. |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| − | ******************* Hier noch ändern ********************** |
||
| + | <br><br> |
||
| − | As we can see on Figure ?, there are a lot of beta sheets, alpha helices and right-handed alpha helices. The white regions are the regions where no secondary structure can be found, which is right. |
||
=== RMSD matrix === |
=== RMSD matrix === |
||
| − | Next we |
+ | Next we analyzed the RMSD values. Therefore, we used a RMSD matrix. This is useful to see if there are groups of structures over the simulation that share a common structure. These groups will have lower RMSD values withing their group and higher RMSD values compared to structure which are not in the group. |
The following matrix shows the RMSD values of our structures. |
The following matrix shows the RMSD values of our structures. |
||
| − | [[Image:mut485_rmsd_matrix.png|thumb|center|Figure : RMSD matrix of our structures during the simulation]] |
+ | [[Image:mut485_rmsd_matrix.png|thumb|center|Figure 41: RMSD matrix of our structures during the simulation]] |
| + | As you can see in Figure 41, there is one big group which is colored in green at the right top. Furthermore in this group there are some light blue regions which indicate regions with higher density. This shows that there are some structures in the simulations which stay more rigid. Besides, the rest of the matrix displays no regions with outstanding high density. This means that there exist dissimilar structure during the simulation, which is probably caused by the moving of the protein. |
||
| − | ******************* Hier noch ändern ********************** |
||
| + | |||
| − | As you can see in the picture above, there is one big group which is colored in green, but it is not possible to find any very dense groups which all have a very low RMSD compared to each other. Only near on the diagonal there are some structures which are colored in cyan, but in general, most of the structures are colored in green which means a RMSD value of about 0.15 Angstrom. So we can see that there are differences of the protein structure during the simulation and therefore we can conclude that this protein is very flexible. |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
=== cluster analysis === |
=== cluster analysis === |
||
| Line 514: | Line 621: | ||
Next, we started a cluster analysis. First of all, we found 225 different clusters. |
Next, we started a cluster analysis. First of all, we found 225 different clusters. |
||
| − | We visualized all of these cluster structures: |
+ | We visualized all of these cluster structures in Figure 42: |
| − | [[Image:mut485_clusters.png|thumb|center|Figure: |
+ | [[Image:mut485_clusters.png|thumb|center|Figure 42: Visualization of the different clusters]] |
Next we aligned some structures of the cluster and measured the RMSD: |
Next we aligned some structures of the cluster and measured the RMSD: |
||
| Line 527: | Line 634: | ||
|cluster 1 |
|cluster 1 |
||
|cluster 2 |
|cluster 2 |
||
| + | |0.790 |
||
| − | | |
||
|- |
|- |
||
|cluster 1 |
|cluster 1 |
||
|cluster 5 |
|cluster 5 |
||
| + | |0.755 |
||
| − | | |
||
| − | |- |
||
| − | |cluster 30 |
||
| − | |cluster 100 |
||
| − | | |
||
|- |
|- |
||
|} |
|} |
||
| + | The RMSD values of the different structures are very similar, which is displayed in the picture above. Furthermore, the RMSD values of the different structures of the clusters are very low. This indicates that the different structures of the simulation agree mostly. |
||
| + | To have a better insight into the distribution of the RMSD value between the different clusters, we visualize the distribution in Figure 43. |
||
| − | ******************* Hier noch ändern ********************** |
||
| − | The RMSD values of the different structures are very similar, which can be seen in the picture above. Furthermore, the RMSD values of the different structures of the clusters are very low. But if we align structures which are far away in number, the RMSD value increase, which shows us that over the simulation time the differences between the start structure and the simulated structures increase. |
||
| − | Therefore, we can see that the different structures of the simulation are very similar, but over the time they change more and more. |
||
| − | + | [[Image:mut485_rmsd_dist.png|thumb|center|Figure 43: Distribution of the RMSD value over the different clusters]] |
|
| + | Figure 43 displays the distribution of the RMSD. The highest peak is at about 0.16 Angstrom. This means, that most of the structures have a RMSD about 0.16 Angstrom compared to the start structure. This value is not that high, but it is a strong hint, that the protein is flexible during the simulation. |
||
| − | [[Image:mut485_rmsd_dist.png|thumb|center|Figure : Distribution of the RMSD value over the different clusters]] |
||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
| + | === internal RMSD === |
||
| − | ******************* Hier noch ändern ********************** |
||
| − | On Figure ?, it is possible to see, that the distribution is a gaussian distribution, with the highest peak at 0.2 Angstrom. This means, that most of the structures have a RMSD about 0.2 Angstrom compared to the start structure. This value is relatively high, especially if we keep in mind, that both structure are the same structure, and only for one structure the motion over the time was simulated. |
||
| + | The last point in our analysis is the calculation of the internal RMSD values. The internal RMSD describes the distances between the single atoms within the protein, which helps to obtain the structure of the protein. |
||
| + | |||
| + | [[Image:mut485_md_internal_rms.png|thumb|center|Figure 44: Plot of the distance RMS values in the protein.]] |
||
| − | === internal RMSD === |
||
{| border="1" style="text-align:center; border-spacing:0;" |
{| border="1" style="text-align:center; border-spacing:0;" |
||
| Line 566: | Line 671: | ||
|- |
|- |
||
|} |
|} |
||
| + | |||
| + | Figure 44 shows that the RMSD increases consistent during the whole simulation. At the beginning the RMSD is relatively small and then arises very fast till it reaches some kind of stagnation where it rises very slow. There exist some valleys in the plot at different time points. However, it looks similar to the curve of the natural logarithms. The internal RMSD reaches at the end about 0.25 Angstrom, which is not relatively high. Therefore the protein has a big distances to itself. |
||
| + | |||
| + | Back to [[http://i12r-studfilesrv.informatik.tu-muenchen.de/wiki/index.php/Tay-Sachs_Disease Tay-Sachs Disease]]. |
||
| + | <br><br> |
||
Latest revision as of 13:03, 29 September 2011
Contents
- 1 check the trajectory
- 2 Visualize in PyMol
- 3 Create a movie
- 4 energy calculations for pressure, temperature, potential and total energy
- 5 minimum distance between periodic boundary cells
- 6 RMSF for protein and C-alpha
- 7 Radius of gyration
- 8 solvent accessible surface area
- 9 hydrogen-bonds
- 10 Ramachandran plot
- 11 RMSD matrix
- 12 cluster analysis
- 13 internal RMSD
check the trajectory
We checked the trajectory and got following results:
Reading frame 0 time 0.000 # Atoms 96545 Precision 0.001 (nm) Last frame 2000 time 10000.000
Furthermore, we got some detailed results about the different items during the simulation.
| Item | #frames | Timestep (ps) |
| Step | 2001 | 5 |
| Time | 2001 | 5 |
| Lambda | 0 | - |
| Coordinates | 2001 | 5 |
| Velocities | 0 | - |
| Forces | 0 | - |
| Box | 2001 | 5 |
The simulation finished on node 0 Thu September 15 19:12:47 2011.
| Time | ||
| Node (s) | Real (s) | % |
| 22336.000 | 22336.000 | 100% |
| 6h12:00 | ||
The complete simulation needs 6 hours and 12 minutes runtime.
| Performance | |||
| Mnbf/s | GFlops | ns/day | hour/ns |
| 1277.617 | 93.808 | 38.682 | 0.620 |
As you can see in the table above, it takes about 2/3 hour to simulate 1 nano second (ns) of the system. So therefore, it would be possible to simulate about 37 ns in one complete day calculation time.
Back to [Tay-Sachs Disease].
Visualize in PyMol
First of all, we visualized the simulation with ngmx, because it draws bonds based on the topology file. ngmx gave the user the possibility to choose different parameters. Therefore, we decided to visualize the system with following parameters:
| Group 1 | Group 2 |
| System | Water |
| Protein | Ion |
| Backbone | NA |
| MainChain+H | CL |
| SideChain |
Figure 1 shows the visualization with ngmx:
Furthermore, we also want to visualize the structure with PyMol, which can be seen on Figure 2.
Back to [Tay-Sachs Disease].
Create a movie
Next, we want to visualize the protein with PyMol. Therefore, we extracted 1000 frames from the trajectory, leaving out the water and jump over the boundaries to make continuous trajectories.
The program asks for a group as output. We only want to see the protein, therefore we decided to choose group 1.
Here you can see the movie in stick line and cartoon modus.
On Figure 3 and Figure 4, we can see that motion of the protein over time, which was created by the MD simulation.
Back to [Tay-Sachs Disease].
energy calculations for pressure, temperature, potential and total energy
Pressure
| Average (in bar) | 0.998385 |
| Error Estimation | 0.0058 |
| RMSD | 71.0317 |
| Tot-Drift | -0.0436306 |
| Minimum (in bar) | -230.0158 |
| Maximum (in bar) | 243.7419 |
The plot with the pressure distribution of the system can be seen here:
As you can see in Figure 5, the pressure fluctuates in the system around 0 and the amplitude does mostly not exceed 100. Contrary,there are some outliers which reach values of almost 250 and -250 bar. In this cases we are not sure, if a protein works under such a high pressure.
Back to [Tay-Sachs Disease].
Temperature
| Average (in K) | 297.936 |
| Error Estimation | 0.0045 |
| RMSD | 0.940566 |
| Tot-Drift | 0.00654126 |
| Minimum (in K) | 294.99 |
| Maximum (in K) | 301.08 |
The plot with the temperature distribution of the system can be seen here:
Figure 6 displays the distribution of the temperature in the current MD system. In this case the temperature fluctuates around 298K. The maximal occurring amplitude between the average and the outliers temperature is only about 4 K which is not much. But we have to keep in mind, that only some degree difference can affect huge functional loss of a protein. 298 K corresponds to 25°C, which is relatively low for human protein activity, because the highest activity is normally reached at body temperature which is about 36°C.
Back to [Tay-Sachs Disease].
Potential
| Average (in kJ/mol) | -1.28176e+06 |
| Error Estimation | 85 |
| RMSD | 1068.67 |
| Tot-Drift | -536.314 |
| Minimum (in kJ/mol) | -1.28513e+06 |
| Maximum (in kJ/mol) | -1.27769e+06 |
The plot with the potential energy distribution of the system can be seen here:
Figure 7 displays the potential energy of the system which is between -1.28513e+06 and -1.27769e+06. This is a relatively low energy. Therefore, this probably means that the protein is stable. Furthermore, we can suggest, that the protein with such a low energy is stable and able to function. Therefore, our simulation is probably true. Otherwise, if the energy of the simulated system would be too high, we can not trust the results, because the protein is too instable to work.
Back to [Tay-Sachs Disease].
Total energy
| Average (in kJ/mol) | -1.05203e+06 |
| Error Estimation | 83 |
| RMSD | 1308.04 |
| Tot-Drift | -531.275 |
| Minimum (in kJ/mol) | -1.05687e+06 |
| Maximum (in kJ/mol) | -1.04680e+06 |
The plot with the total energy distribution of the system can be seen here:
Looking at Figure 8, we can see that the total energy deviates a little from the potential energy which is minimal lower. In this case, the total energy is between -1.055e+06 and -1.045e+06. These values lie already in a range, where we can suggest that the protein energy is sufficient low so that this one can work.
Back to [Tay-Sachs Disease].
minimum distance between periodic boundary cells
Next we try to calculate the minimum distance between periodic boundary cells. As before, the program asks for one group to use for the calculation and we decided to use only the protein, because the calculation needs a lot of time and the whole system is significant bigger than only the protein. So therefore, we used group 1.
Here you can see the result of this analysis:
| Average (in nm) | 3.215 |
| Minimum | 1.772 |
| Maximum | 4.217 |
Figure 9 displays the minimum distance between periodic boundary cells at different time steps. It can be seen that there are huge differences between the distances at different times. The highest distance is 4.217 nm, whereas the smallest distance is only 1.772 nm. This means that there are some states during the simulation in which the interacting atoms are close together. Contrary, there are some states in which the atoms who interact are far away. Because of the huge bandwidth of minimum distance we can conclude, that the protein is flexible.
Back to [Tay-Sachs Disease].
RMSF for protein and C-alpha
Protein
First of all, we calculate the RMSF for the whole protein.
The analysis produce two different pdb files, one file with the average structure of the protein and one file with high B-Factor values, which means that the high flexible regions of the protein are not in accordance with the original PDB file.
To compare the structure we align them with PyMol to the original structure.
| original & average | original & B-Factors | average & B-Factors |
| Perspective one | ||
| Perspective two | ||
| RMSD | ||
| 1.519 | 0.349 | 1.727 |
The RMSD as well as the structure alignment visualization indicates which structures are similar. In this case, the small RMSD at 0.349 as well as the structure alignment where the structures mostly agree indicates that the high B-factors agrees mostly with the original structure (Figure 11 and 14). The alignment of the original structure and the average structure delivers a higher disagreement (Figure 10 and Figure 13). There, the RMSD with 1.519 is much higher and the structure alignment is not extremely worse than the other one. The regions with high B-Factors are usually very flexible. This means that the downloaded PDB structure is probably in another state, because of its flexible regions. The low RMSD and the agreeing structure alignment of the high B-factor structure and the original one displays that the quality of predicted structure is quite good.
Furthermore, we got a plot of the RMSF values of the protein, which can be seen in Figure 13:
There are two regions with very high RMSF values. The first one is at position 150 (Figure 17), and the second one is at position 350 (Figure 18). The structure alignment of the average structure and the original one shows that the most regions match with some exceptions. Therefore, we want to analysis, if these bad-matching regions are the regions with very high B-factor values. The following picture show the two regions around position 150 and 350 which have an arose RMSF.
Furthermore, we visualized the B-factors with the PyMol selection B-factor method at these two regions. We calculated the B-factors for the blue protein (Figure 19 and Figure 20). If you see red, this part of the protein is very flexible. The brighter the color, the higher is the flexibility of this residue.
The first picture displays the alignment around region 150. Here, we can see that the loop is colored in yellow and red. This bright colors show that the B-factor at this position is very high which indicates a higher flexibility. Contrary, the second picture for the region around residue 350 show only a small part in yellow and some parts in turquoise whereas the rest is colored in dark blue. Furthermore, the second peak is about 0.35 which does not stand for a high flexibility. All in all, this detailed views assume that there is only one region in the protein with a high flexibility.
As you can see at the pictures above, especially at the first picture, which is the part with the highest peak in the plot, the structures have a very different position and the alignment in this part of the protein is very bad, although the rest of the alignment is quite good. That is also the reason for the relatively high RMSD which is caused by different position of the flexible parts of the protein.
Back to [Tay-Sachs Disease].
C-alpha
Now we repeat the analysis, done for the protein, for the C-alpha atoms of the protein. Therefore, we followed the same steps as in the section above.
To compare the structure we align them with PyMol with the original structure.
| original & average | original & B-Factors | average & B-Factors |
| Perspective one | ||
| Perspective two | ||
| RMSD | ||
| 1.258 | 0.283 | 1.297 |
As in the section above, the RMSD between the structure with high B-factor values and the original structure is the most similar (Figure 22 and Figure 25). This was expected, because we used twice the same model, but in this case we neglected the residues of the atoms whereas the backbone of the protein remains the same. The other two models (Figure 21, Figure 23, Figure 24 and Figure 26) have nearly the same RMSD value and therefore there are equally.
Furthermore, we got a plot of the RMSF values of the protein, which can be seen on Figure 24:
In this case, there is only one high peak at position 150 (Figure 27). Having a closer look at the protein it can be seen that the position of the beta sheets differ extremely between the two models. The other peak at position 350 could not be found in the plot. Looking at the pictures above, we can see that the backbones of the two different models not differ extremely. This means that the position of the residues differ a lot, which is not important for us, because we do not regard side chains.
Radius of gyration
Next, we want to analyze the Radius of gyration. Therefore we use g_gyrate and use only the protein for the calculation.
| Rg (in nm) | RgX (in nm) | RgY (in nm) | RgZ (in nm) | |
| Average | 2.416 | 2.145 | 1.630 | 2.094 |
| Minimum | 2.347 | 1.992 | 1.444 | 1.809 |
| Maximum | 2.449 | 2.212 | 1.927 | 2.219 |
Figure 28 shows the radius of gyration over the simulation time. The radius of gyration is the RMS distance from the outer parts of the protein to the protein center or gyration axis. The plot displays that the average radius is about 2.42 with some fluctuation. This indicates that the protein is flexible. Furthermore, the fluctuation is a periodic curve which shows the loss and the gain of space the protein needs. This suggest that the protein pulsates.
If we have a further look at the radius of the different axis (Figure 29), we can see, that the radius of the x coordinates is the only consistent one at about 2nm during the simulation. The radius of the z axis shows deflection at the end of the simulation where it decreases. The y axis values, however, increase during the simulation and reaches the value of the decreased z-radius which is still smaller than the radius for the x-axis. This means that the motions in x and the motion in z at the beginning of the simulation has most influence on the whole gyration radius.
Back to [Tay-Sachs Disease].
solvent accessible surface area
Next, we analyzed the solvent accessible surface area of the protein, which is the area of the protein which has contacts with the surrounding environment, mainly water.
First of all, we have a look at the solvent accessibility of each residue, which can be seen on Figure 27. Furthermore, we regard at the solvent accessibility area of each residue in the protein with standard deviation (Figure 28).
The following table list the average, minimum and maximum values of the solvent accessibility for each residue in the protein. The residues at the beginning and at the end of the simulation which have a value of 0 are ignored.
| Average (in nm²) | 0.542 |
| Minimum (in nm²) | 0.007 |
| Maximum (in nm²) | 2.014 |
The average area per residue during the trajectory is between 0 and 2nm², as can be seen in Figure 30. Most of the residues have an area about 0.5nm². From this it follows that there are mainly sparse moving residues during the complete simulation with some exceptions where the residues are very flexible. In Figure 31, you can additionally see the standard deviation, which is very low and which indicates that there are no big outliers in there. This means that there is no big deviation from the average area so the residues behave in the same way during the trajectory.
Besides, we can analyze the position of the residues within the protein based on the solvent accessibility. First, we can see in Figure 30 that the first 100 and the last 100 residues have an average solvent accessibility of 0 which means that these residues are always completely in the interior of the protein. Most of the residues have a solvent accessibility about 0.5nm², and there are only some outliers with an accessibility of more than 1.5nm². This means that there are some residues which are almost always on the surface, a lot of residues which are partly or temporarily on the surface and a lot of residues which are never on the surface. Looking at Figure 31, we can see that the standard deviation is relatively low. This means that there are no system states in which any residues with low or no solvent accessibility get complete accessible to the surface. If the standard deviation would be very high, it would indicate that there are some very unusual states in the simulation which is not the case in our simulation.
Furthermore, it is possible to look at the solvent accessibility of each atom of the complete protein, which can be seen in Figure 32 and Figure 33.
As before, we only regard the atoms with an area of more than 0 in the following table.
| Average (in nm²) | 0.032 |
| Minimum (in nm²) | 0 |
| Maximum (in nm²) | 0.561 |
In Figure 32 the average area per atom is plotted, which deliver similar results to Figure 30. In general the atoms have not such a big area as the residues. This can be explained easily because the residue area is consisting of the single atom areas which belong to this residue. There are a huge number of atoms which have an area of about 0nm². As before, the standard deviation is not that high (Figure 33). It is a little bit higher than than the one in Figure 28 which was expected, because of the smaller and more detailed scale of this Figure. In general Figure 32 and Figure 33 confirm the results of Figure 30 and Figure 31.
At the end of the plot, there are a lot of atoms which have a surface accessibility area of 0, which is consistent with the result for the residues. But at the beginning of the plot, there are no atoms which have no surface accessibility area. However, there are a lot of atoms with low or no accessibility area in the plot.
Figure 34 shows how much of the area of the protein is accessible to the surface during the complete simulation. As we saw before, by the gyration radius of the protein, the values differ during the simulation, which shows, that the protein is flexible.
| Average (in nm²) | 135.452 |
| Minimum (in nm²) | 129.167 |
| Maximum (in nm²) | 142.977 |
Figure 34 and Figure 35 display the solvent accessibility surface of the whole protein during the simulation. The surface accessibility of the hydrophobic residues has an area of about 135nm², which is relatively consistent during the complete simulation. The second plot describes the solvent accessibility for different physicochemical properties. It shows that the accessibility rate of the hydrophobic amino acids is larger than of the hydrophilic amino acids which is unexpected. Normally, hydrophobic amino acids prefer a location in the core of the protein and not on the surface.
Back to [Tay-Sachs Disease].
hydrogen-bonds
As a next step we analysis the formed hydrogen bonds within the protein during the simulation. Here, we differ between hydrogen-bonds between the protein itself and bonds between the protein and the water.
The following plots display the number of hydrogen bonds within the protein over the simulation time.
| bonds in the protein | possible bonds in the protein | |
| Average | 323.337 | 1543.024 |
| Minimum | 300 | 1491 |
| Maximum | 354 | 1602 |
In Figure 36 you can see the bonds within the protein. Here the number differs between 300 bonds and 355. Most of the time, the protein has between 320 and 330 hydrogen-bonds. Furthermore, it is possible to see in this plot, that the protein is flexible, because the number of bonds fluctuate extremely over the time.
Figure 37 displays the number of hydrogen bonds that occur during the simulation as well as all residue pairs with a distance smaller than 0.35nm which is the distance where a hydrogen bond is theoretically possible. This plot shows that there exist much more possible hydrogen bindings than occurred in real. Here the number of possible pairs is about 1500 whereas the number of formed hydrogen bond is only between 320 and 330 which is only about 20%. The small number of formed hydrogen bonds can indicate the high protein's flexibility.
The following plots display the number of hydrogen bonds between the protein and the surrounding water over the simulation time.
| bonds between protein and water | possible bonds between protein and water | |
| Average | 847.965 | 999.310 |
| Minimum | 783 | 882 |
| Maximum | 912 | 1126 |
Looking at the number of hydrogen bonds formed between the protein and the surrounding water, which is visualized in Figure 38, we can see that there exist much more bonds between protein and water than within the protein. The number differs between 800 and 900 which is about 3 times more than the number within the protein. Most of the time, the protein forms between 840 and 860 bonds with the surrounding water.
Figure 39 displays additional the number of residue pairs with a distance less than 0.35 nm which is the distance where a hydrogen bond is theoretically possible. The number of pairs within 0.35nm is about 1000. Compared to Figure 34 the distance of possible and real occurring hydrogen bonds is significantly lower. In this case, almost 80% of all possible hydrogen bonds are also real hydrogen bonds. Therefore, we can see that the binding between protein and water is really stable.
This is no surprise, because every residue on the surface has contact with water, whereas within the protein there are a lot of amino acids which have no contact partners, because of the big underlying distance to another amino acid.
Back to [Tay-Sachs Disease].
Ramachandran plot
Now, we want to have a closer look to the secondary structure of the protein during the simulation. Therefore, we used a Ramachandran plot to analyze the phi and psi torsion angles of the backbone to get a better understanding of the secondary structure during the simulation.
As we can see on Figure 40, there are a lot of beta sheets, alpha helices and right-handed alpha helices. The white regions are the regions where no secondary structure can be found. The white regions of our ramachandran plot agree with the white regions of a standard ramachandran plot.
Back to [Tay-Sachs Disease].
RMSD matrix
Next we analyzed the RMSD values. Therefore, we used a RMSD matrix. This is useful to see if there are groups of structures over the simulation that share a common structure. These groups will have lower RMSD values withing their group and higher RMSD values compared to structure which are not in the group.
The following matrix shows the RMSD values of our structures.
As you can see in Figure 41, there is one big group which is colored in green at the right top. Furthermore in this group there are some light blue regions which indicate regions with higher density. This shows that there are some structures in the simulations which stay more rigid. Besides, the rest of the matrix displays no regions with outstanding high density. This means that there exist dissimilar structure during the simulation, which is probably caused by the moving of the protein.
Back to [Tay-Sachs Disease].
cluster analysis
Next, we started a cluster analysis. First of all, we found 225 different clusters.
We visualized all of these cluster structures in Figure 42:
Next we aligned some structures of the cluster and measured the RMSD:
| Cluster 1 | Cluster 2 | RMSD |
| cluster 1 | cluster 2 | 0.790 |
| cluster 1 | cluster 5 | 0.755 |
The RMSD values of the different structures are very similar, which is displayed in the picture above. Furthermore, the RMSD values of the different structures of the clusters are very low. This indicates that the different structures of the simulation agree mostly.
To have a better insight into the distribution of the RMSD value between the different clusters, we visualize the distribution in Figure 43.
Figure 43 displays the distribution of the RMSD. The highest peak is at about 0.16 Angstrom. This means, that most of the structures have a RMSD about 0.16 Angstrom compared to the start structure. This value is not that high, but it is a strong hint, that the protein is flexible during the simulation.
Back to [Tay-Sachs Disease].
internal RMSD
The last point in our analysis is the calculation of the internal RMSD values. The internal RMSD describes the distances between the single atoms within the protein, which helps to obtain the structure of the protein.
| Average (RMSD in nm) | 0.243 |
| Minimum (RMSD in nm) | 4.906e-07 |
| Maximum (RMSD in nm) | 0.289 |
Figure 44 shows that the RMSD increases consistent during the whole simulation. At the beginning the RMSD is relatively small and then arises very fast till it reaches some kind of stagnation where it rises very slow. There exist some valleys in the plot at different time points. However, it looks similar to the curve of the natural logarithms. The internal RMSD reaches at the end about 0.25 Angstrom, which is not relatively high. Therefore the protein has a big distances to itself.
Back to [Tay-Sachs Disease].